本书对多元积分的处理是先推广一元黎曼积分,本节仅对黎曼积分的一些大家熟知的概念作了推广,包括partition以及黎曼和等。比较重要的是Theorem 10.3(Riemann condition),下积分和上积分相等的充要条件,与一元黎曼积分几乎完全类似。Theorem 10.4是黎曼条件的一个小应用,证明常数函数是可积的。
Exercises
Exercise 1. Let  be bounded functions such that
be bounded functions such that  for
for  . Show that
. Show that  and
and  .
.
Solution: As  , for any
, for any 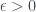 , we can find a partition
, we can find a partition  such that
such that

and it follows that  .
.
Exercise 2. Suppose  is continuous. Show
is continuous. Show  is integrable over
is integrable over 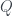 .
.
Solution: We suppose  , then
, then 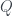 is bounded, and
is bounded, and  is in fact uniformly continuous on
is in fact uniformly continuous on 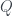 , thus for any
, thus for any 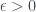 , there is a
, there is a  such that
such that

Choose a partition  with
with  for
for  , then within each subrectangle contained in
, then within each subrectangle contained in  ,
,  would have diversion at most
would have diversion at most  , thus
, thus

Exercise 3. Let ![[0,1]^2=[0,1]\times [0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%5E2%3D%5B0%2C1%5D%5Ctimes+%5B0%2C1%5D&bg=ffffff&fg=333A42&s=0&c=20201002) . Let
. Let ![f:[0,1]^2\to\mathbf{R}](https://s0.wp.com/latex.php?latex=f%3A%5B0%2C1%5D%5E2%5Cto%5Cmathbf%7BR%7D&bg=ffffff&fg=333A42&s=0&c=20201002) be defined by setting
be defined by setting  if
if  , and
, and  if
if  . Show that
. Show that  is integrable over
is integrable over ![[0,1]^2](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%5E2&bg=ffffff&fg=333A42&s=0&c=20201002) .
.
Solution: For any 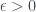 , let
, let ![N=[1/\epsilon]+1](https://s0.wp.com/latex.php?latex=N%3D%5B1%2F%5Cepsilon%5D%2B1&bg=ffffff&fg=333A42&s=0&c=20201002) , and
, and  , let
, let  , we see that
, we see that  and
and  only diverges in rectangles
only diverges in rectangles ![R_k=[k/N,(k+1)/N]\times [k/N,(k+1)/N]](https://s0.wp.com/latex.php?latex=R_k%3D%5Bk%2FN%2C%28k%2B1%29%2FN%5D%5Ctimes+%5Bk%2FN%2C%28k%2B1%29%2FN%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , in which
, in which 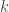 ranges from
ranges from 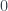 to
to  and
and  , thus
, thus

Exercise 4. We say ![f:[0,1]\to\mathbf{R}](https://s0.wp.com/latex.php?latex=f%3A%5B0%2C1%5D%5Cto%5Cmathbf%7BR%7D&bg=ffffff&fg=333A42&s=0&c=20201002) is increasing if
is increasing if  whenever
whenever  . If
. If ![f,g:[0,1]\to\mathbf{R}](https://s0.wp.com/latex.php?latex=f%2Cg%3A%5B0%2C1%5D%5Cto%5Cmathbf%7BR%7D&bg=ffffff&fg=333A42&s=0&c=20201002) are increasing and non-negative, show that the function
are increasing and non-negative, show that the function  is integrable over
is integrable over ![[0,1]^2](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D%5E2&bg=ffffff&fg=333A42&s=0&c=20201002) .
.
Solution: Both  and
and 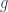 are integrable over
are integrable over ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , which means
, which means ![\int_{[0,1]}f](https://s0.wp.com/latex.php?latex=%5Cint_%7B%5B0%2C1%5D%7Df&bg=ffffff&fg=333A42&s=0&c=20201002) and
and ![\int_{[0,1]}g](https://s0.wp.com/latex.php?latex=%5Cint_%7B%5B0%2C1%5D%7Dg&bg=ffffff&fg=333A42&s=0&c=20201002) exist.
exist.
For any 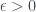 , let
, let  be an integer and
be an integer and  , let
, let  , we see that
, we see that
![\displaystyle{U(f,P)-L(f,P)=\frac{1}{n^2}\left[(f(1)-f(0))\left(g\left(\frac{1}{n}\right)+\cdots+g(1)\right)+(g(1)-g(0))\left(f\left(\frac{1}{n}\right)+\cdots+f(1)\right)\right]}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%7BU%28f%2CP%29-L%28f%2CP%29%3D%5Cfrac%7B1%7D%7Bn%5E2%7D%5Cleft%5B%28f%281%29-f%280%29%29%5Cleft%28g%5Cleft%28%5Cfrac%7B1%7D%7Bn%7D%5Cright%29%2B%5Ccdots%2Bg%281%29%5Cright%29%2B%28g%281%29-g%280%29%29%5Cleft%28f%5Cleft%28%5Cfrac%7B1%7D%7Bn%7D%5Cright%29%2B%5Ccdots%2Bf%281%29%5Cright%29%5Cright%5D%7D&bg=ffffff&fg=333A42&s=0&c=20201002)
Notice that we can choose 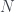 such that when
such that when  ,
,
![\displaystyle{\left|\frac{g(1/n)+\cdots+g(1)}{n}-\int_{[0,1]}g\right|<1,\left|\frac{f(1/n)+\cdots+f(1)}{n}-\int_{[0,1]}f\right|<1}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%7B%5Cleft%7C%5Cfrac%7Bg%281%2Fn%29%2B%5Ccdots%2Bg%281%29%7D%7Bn%7D-%5Cint_%7B%5B0%2C1%5D%7Dg%5Cright%7C%3C1%2C%5Cleft%7C%5Cfrac%7Bf%281%2Fn%29%2B%5Ccdots%2Bf%281%29%7D%7Bn%7D-%5Cint_%7B%5B0%2C1%5D%7Df%5Cright%7C%3C1%7D&bg=ffffff&fg=333A42&s=0&c=20201002)
thus the expression
![\displaystyle{\frac{1}{n}\left[(f(1)-f(0))\left(g\left(\frac{1}{n}\right)+\cdots+g(1)\right)+(g(1)-g(0))\left(f\left(\frac{1}{n}\right)+\cdots+f(1)\right)\right]}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%7B%5Cfrac%7B1%7D%7Bn%7D%5Cleft%5B%28f%281%29-f%280%29%29%5Cleft%28g%5Cleft%28%5Cfrac%7B1%7D%7Bn%7D%5Cright%29%2B%5Ccdots%2Bg%281%29%5Cright%29%2B%28g%281%29-g%280%29%29%5Cleft%28f%5Cleft%28%5Cfrac%7B1%7D%7Bn%7D%5Cright%29%2B%5Ccdots%2Bf%281%29%5Cright%29%5Cright%5D%7D&bg=ffffff&fg=333A42&s=0&c=20201002)
is in fact bounded, we can choose  large enough to guarantee
large enough to guarantee  , and the conclusion follows.
, and the conclusion follows.
Exercise 5. Let  be defined by setting
be defined by setting  if
if  , where
, where 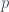 and
and  are positive integers with no common factor, and
are positive integers with no common factor, and  otherwise, show
otherwise, show  is integrable over
is integrable over ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333A42&s=0&c=20201002) .
.
Solution: Since  only take nonzero values on
only take nonzero values on ![Q\cap[0,1]](https://s0.wp.com/latex.php?latex=Q%5Ccap%5B0%2C1%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , we see that
, we see that  for any partition
for any partition  of
of ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333A42&s=0&c=20201002) . For any
. For any 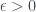 , let
, let  and
and  be a partition of
be a partition of ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , notice that there will be only
, notice that there will be only  rectangles in the sum of
rectangles in the sum of  , and the value
, and the value  would be the supremum of
would be the supremum of  for some rectangle only if all the value
for some rectangle only if all the value  have been the supremum of
have been the supremum of  for some rectangle in
for some rectangle in  , and each value
, and each value  would occur
would occur  times for
times for  , thus each rectangle which take the supremum value
, thus each rectangle which take the supremum value  would amount at most
would amount at most  , and the total contribution in the sum
, and the total contribution in the sum  would be
would be  , thus
, thus  .
.
Exercise 6. Prove the following:
Theorem. Let  be bounded. Then
be bounded. Then  is integrable over
is integrable over 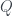 if and only if given
if and only if given 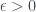 , there is a
, there is a  such that
such that  for every partition
for every partition  of mesh less than
of mesh less than  .
.
Proof. ( a ) Verify the “if” part of the theorem.
( b ) Suppose  for
for  . Let
. Let  be a partition of
be a partition of 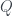 . Show that if
. Show that if  is obtained by adjoining a single point to the partition of one of the component intervals of
is obtained by adjoining a single point to the partition of one of the component intervals of 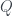 , then
, then

Derive a similar result for upper sums.
( c ) Prove the “only if” part of the theorem: Suppose  is integrable over
is integrable over 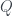 . Given
. Given 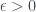 , choose a partition
, choose a partition  such that
such that  . Let
. Let 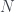 be the number of partition points in
be the number of partition points in  ; then let
; then let  . Show that if
. Show that if  has mesh less than
has mesh less than  , then
, then  .
.
Solution:
( a ) The “if” part is easy from the definition.
( b ) If  is obtained by adjoining a single point to the partition of one of the component intervals
is obtained by adjoining a single point to the partition of one of the component intervals ![[a_i,b_i]](https://s0.wp.com/latex.php?latex=%5Ba_i%2Cb_i%5D&bg=ffffff&fg=333A42&s=0&c=20201002) of
of 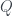 , if
, if  , without loss of generality we suppose this single point is added in the interval
, without loss of generality we suppose this single point is added in the interval  , then
, then and
and  only differs in subrectangles with the form
only differs in subrectangles with the form

The point divides  into
into  and
and  , let
, let  denote the length of an interval
denote the length of an interval  , we have
, we have  . For an specific subrectangle
. For an specific subrectangle  which is being divided, we see that
which is being divided, we see that

If  reaches local minimum at
reaches local minimum at  and
and  , then
, then  reaches local minimum at
reaches local minimum at  in
in  , vice versa, in the first case we suppose in
, vice versa, in the first case we suppose in  the local minimum of
the local minimum of  occurs at
occurs at 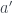 , then the contribution in
, then the contribution in  takes the form
takes the form

while the contribution in  takes the form
takes the form

Compare the difference we have
![\displaystyle{\begin{aligned}V_2-V_1&=f(a)[L(I')-L(I)]v( I_2\times\cdots\times I_n)+f(a')L(I'')v( I_2\times\cdots\times I_n)\\&=[f(a')-f(a)]L(I'')v( I_2\times\cdots\times I_n)\\&\leq2M(\text{mesh }P)v( I_2\times\cdots\times I_n)\end{aligned}}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%7B%5Cbegin%7Baligned%7DV_2-V_1%26%3Df%28a%29%5BL%28I%27%29-L%28I%29%5Dv%28+I_2%5Ctimes%5Ccdots%5Ctimes+I_n%29%2Bf%28a%27%29L%28I%27%27%29v%28+I_2%5Ctimes%5Ccdots%5Ctimes+I_n%29%5C%5C%26%3D%5Bf%28a%27%29-f%28a%29%5DL%28I%27%27%29v%28+I_2%5Ctimes%5Ccdots%5Ctimes+I_n%29%5C%5C%26%5Cleq2M%28%5Ctext%7Bmesh+%7DP%29v%28+I_2%5Ctimes%5Ccdots%5Ctimes+I_n%29%5Cend%7Baligned%7D%7D&bg=ffffff&fg=333A42&s=0&c=20201002)
As  goes through
goes through  , we have
, we have

A similar result can be derived for upper sums, i.e. if  is obtained by adjoining a single point to the partition of one of the component intervals of
is obtained by adjoining a single point to the partition of one of the component intervals of 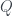 , then
, then

( c ) If  has mesh less than
has mesh less than  , then we add the
, then we add the 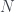 points of
points of  to get a refinement of
to get a refinement of  and
and  , namely
, namely  , we have
, we have

Similarly we have  , thus using the fact that
, thus using the fact that  is a refinement of
is a refinement of  ‘, we have
‘, we have

Exercise 7. Use Exercise 6 to prove the following:
Theorem. Let  be bounded. Then the statement that
be bounded. Then the statement that  is integrable over
is integrable over 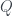 , with
, with  , is equivalent to the statement that given
, is equivalent to the statement that given 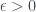 , there is a
, there is a  such that if
such that if  is any partition of mesh less than
is any partition of mesh less than  , and if for each subrectangle
, and if for each subrectangle  determined by
determined by  ,
,  is a point of
is a point of  , then
, then

Solution: If  is integrable over
is integrable over 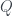 , then by Exercise 6, given
, then by Exercise 6, given 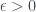 there is a
there is a  such that if
such that if  is any partition of mesh less than
is any partition of mesh less than  , we have
, we have  , notice that
, notice that  and for each subrectangle
and for each subrectangle  determined by
determined by  we have
we have

the “if” part of the theorem is proved. Conversely, given 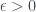 , we first find a
, we first find a  such that for each subrectangle
such that for each subrectangle  determined by
determined by  which has mesh less than
which has mesh less than  :
:

then  and
and  , which means
, which means  , so
, so  is integrable by Exercise 6. Assume
is integrable by Exercise 6. Assume  , then let
, then let  we can easily deduce a contradiction.
we can easily deduce a contradiction.