Exercise 11.10.1. Prove Proposition 11.10.1.
Proposition 11.10.1 (Integration by parts formula). Let ![I=[a,b]](https://s0.wp.com/latex.php?latex=I%3D%5Ba%2Cb%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , and let
, and let ![F:[a,b]\to\mathbf R](https://s0.wp.com/latex.php?latex=F%3A%5Ba%2Cb%5D%5Cto%5Cmathbf+R&bg=ffffff&fg=333A42&s=0&c=20201002) and
and ![G:[a,b]\to\mathbf R](https://s0.wp.com/latex.php?latex=G%3A%5Ba%2Cb%5D%5Cto%5Cmathbf+R&bg=ffffff&fg=333A42&s=0&c=20201002) be differentiable functions on
be differentiable functions on ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=333A42&s=0&c=20201002) such that
such that  and
and  are Riemann integrable on
are Riemann integrable on  . Then we have
. Then we have
![\displaystyle{\int_{[a,b]}FG'=F(b)G(b)-F(a)G(a)-\int_{[a,b]}F'G}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%7B%5Cint_%7B%5Ba%2Cb%5D%7DFG%27%3DF%28b%29G%28b%29-F%28a%29G%28a%29-%5Cint_%7B%5Ba%2Cb%5D%7DF%27G%7D&bg=ffffff&fg=333A42&s=0&c=20201002) .
.
Solution: As  and
and 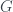 are differentiable, they are continuous on
are differentiable, they are continuous on ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=333A42&s=0&c=20201002) and thus Riemann integrable by Corollary 11.5.2, then
and thus Riemann integrable by Corollary 11.5.2, then  and
and  are Riemann integrable by Theorem 11.4.5. Notice that
are Riemann integrable by Theorem 11.4.5. Notice that  and
and  is Riemann integrable on
is Riemann integrable on ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , we can use the second fundamental theorem of calculus to have
, we can use the second fundamental theorem of calculus to have
![\displaystyle{\int_{[a,b]}(F'G+FG')=(FG)(b)-(FG)(a)}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%7B%5Cint_%7B%5Ba%2Cb%5D%7D%28F%27G%2BFG%27%29%3D%28FG%29%28b%29-%28FG%29%28a%29%7D&bg=ffffff&fg=333A42&s=0&c=20201002)
By some simple calculation we can have the final result.

Exercise 11.10.2. fill in the gaps marked (why?) in the proof of Lemma 11.10.5.
Lemma 11.10.5 (Change of variables formula I). Let ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=333A42&s=0&c=20201002) be a closed interval, and let
be a closed interval, and let ![\phi:[a,b]\to [\phi (a),\phi (b)]](https://s0.wp.com/latex.php?latex=%5Cphi%3A%5Ba%2Cb%5D%5Cto+%5B%5Cphi+%28a%29%2C%5Cphi+%28b%29%5D&bg=ffffff&fg=333A42&s=0&c=20201002) be a continuous monotone increasing function. Let
be a continuous monotone increasing function. Let ![f:[\phi (a),\phi (b)]\to\mathbf R](https://s0.wp.com/latex.php?latex=f%3A%5B%5Cphi+%28a%29%2C%5Cphi+%28b%29%5D%5Cto%5Cmathbf+R&bg=ffffff&fg=333A42&s=0&c=20201002) be a piecewise constant function on
be a piecewise constant function on ![[\phi (a),\phi (b)]](https://s0.wp.com/latex.php?latex=%5B%5Cphi+%28a%29%2C%5Cphi+%28b%29%5D&bg=ffffff&fg=333A42&s=0&c=20201002) . Then
. Then ![f\circ \phi:[a,b]\to\mathbf R](https://s0.wp.com/latex.php?latex=f%5Ccirc+%5Cphi%3A%5Ba%2Cb%5D%5Cto%5Cmathbf+R&bg=ffffff&fg=333A42&s=0&c=20201002) is also piecewise constant on
is also piecewise constant on ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , and
, and
![\displaystyle{\int_{[a,b]}f\circ \phi d\phi =\int_{[\phi (a),\phi (b)]}f}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%7B%5Cint_%7B%5Ba%2Cb%5D%7Df%5Ccirc+%5Cphi+d%5Cphi+%3D%5Cint_%7B%5B%5Cphi+%28a%29%2C%5Cphi+%28b%29%5D%7Df%7D&bg=ffffff&fg=333A42&s=0&c=20201002) .
.
Solution: I will prove Lemma 11.10.5 completely.
Let  be a partition of
be a partition of ![[{\phi}(a),{\phi}(b)]](https://s0.wp.com/latex.php?latex=%5B%7B%5Cphi%7D%28a%29%2C%7B%5Cphi%7D%28b%29%5D&bg=ffffff&fg=333A42&s=0&c=20201002) such that
such that  is piecewise constant with respect to
is piecewise constant with respect to  . we may assume that
. we may assume that  does not contain the empty set. For each
does not contain the empty set. For each  , let
, let  be the constant value of
be the constant value of  on
on 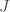 , thus
, thus
![\displaystyle{\int_{[{\phi}(a),{\phi}(b)]} f=\sum_{J\in \mathbf P}c_J |J|}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%7B%5Cint_%7B%5B%7B%5Cphi%7D%28a%29%2C%7B%5Cphi%7D%28b%29%5D%7D+f%3D%5Csum_%7BJ%5Cin+%5Cmathbf+P%7Dc_J+%7CJ%7C%7D&bg=ffffff&fg=333A42&s=0&c=20201002)
For each interval 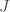 , let
, let ![{\phi}^{-1} (J):=\{x\in [a,b]:{\phi}(x)\in J\}](https://s0.wp.com/latex.php?latex=%7B%5Cphi%7D%5E%7B-1%7D+%28J%29%3A%3D%5C%7Bx%5Cin+%5Ba%2Cb%5D%3A%7B%5Cphi%7D%28x%29%5Cin+J%5C%7D&bg=ffffff&fg=333A42&s=0&c=20201002) . Then given any
. Then given any  , we have
, we have  by the definition of
by the definition of  , and
, and  since
since  is monotone increasing, and
is monotone increasing, and ![\forall z\in [x,y]](https://s0.wp.com/latex.php?latex=%5Cforall+z%5Cin+%5Bx%2Cy%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , we have
, we have  again by
again by  is monotone increasing, this means
is monotone increasing, this means  since
since 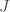 is an interval, so
is an interval, so  is connected, and thus is an interval. Furthermore, if
is connected, and thus is an interval. Furthermore, if  , then
, then  and
and  , thus
, thus  is the constant value of
is the constant value of  on
on  .
.
Thus if we define  , then for any
, then for any ![c\in [a,b], {\phi}(c)\in [{\phi}(a),{\phi}(b)]](https://s0.wp.com/latex.php?latex=c%5Cin+%5Ba%2Cb%5D%2C+%7B%5Cphi%7D%28c%29%5Cin+%5B%7B%5Cphi%7D%28a%29%2C%7B%5Cphi%7D%28b%29%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , so there is a
, so there is a  such that
such that  , which means
, which means  . Assume we can find two sets
. Assume we can find two sets  s.t.
s.t.  , then it means we can find
, then it means we can find  s.t.
s.t.  , contradict the fact that
, contradict the fact that  is a partition of
is a partition of ![[{\phi}(a),{\phi}(b)]](https://s0.wp.com/latex.php?latex=%5B%7B%5Cphi%7D%28a%29%2C%7B%5Cphi%7D%28b%29%5D&bg=ffffff&fg=333A42&s=0&c=20201002) . We can conclude
. We can conclude 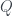 is a partition of
is a partition of ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=333A42&s=0&c=20201002) .
.
Given any  , we have
, we have  for some
for some  , so
, so  is the constant value of
is the constant value of  on this
on this 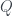 , which means
, which means  piecewise constant with respect to
piecewise constant with respect to  . Thus
. Thus
![\displaystyle{\int_{[a,b]}f\circ {\phi} d{\phi}=\int_{[\mathbf Q]}f\circ {\phi} d{\phi}=\sum_{J\in \mathbf P}c_J {\phi}[{\phi}^{-1}(J)] }](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%7B%5Cint_%7B%5Ba%2Cb%5D%7Df%5Ccirc+%7B%5Cphi%7D+d%7B%5Cphi%7D%3D%5Cint_%7B%5B%5Cmathbf+Q%5D%7Df%5Ccirc+%7B%5Cphi%7D+d%7B%5Cphi%7D%3D%5Csum_%7BJ%5Cin+%5Cmathbf+P%7Dc_J+%7B%5Cphi%7D%5B%7B%5Cphi%7D%5E%7B-1%7D%28J%29%5D+%7D&bg=ffffff&fg=333A42&s=0&c=20201002)
To calculate ![{\phi}[{\phi}^{-1}(J)]](https://s0.wp.com/latex.php?latex=%7B%5Cphi%7D%5B%7B%5Cphi%7D%5E%7B-1%7D%28J%29%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , we let
, we let  , then
, then 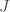 is an interval with endpoints
is an interval with endpoints  , and
, and  , as
, as  is monotone increasing, we can find
is monotone increasing, we can find  , s.t.
, s.t.  , and
, and  is an interval which has endpoints
is an interval which has endpoints  , thus
, thus ![{\phi}[{\phi}^{-1}(J)]={\phi}(b' )-{\phi}(a')=b-a=|J|](https://s0.wp.com/latex.php?latex=%7B%5Cphi%7D%5B%7B%5Cphi%7D%5E%7B-1%7D%28J%29%5D%3D%7B%5Cphi%7D%28b%27+%29-%7B%5Cphi%7D%28a%27%29%3Db-a%3D%7CJ%7C&bg=ffffff&fg=333A42&s=0&c=20201002) , and the claim follows.
, and the claim follows.

Exercise 11.10.3. Let  be real numbers, and let
be real numbers, and let ![f:[a,b]\to\mathbf R](https://s0.wp.com/latex.php?latex=f%3A%5Ba%2Cb%5D%5Cto%5Cmathbf+R&bg=ffffff&fg=333A42&s=0&c=20201002) be Riemann integrable function. Let
be Riemann integrable function. Let ![g:[-b,-a]\to\mathbf R](https://s0.wp.com/latex.php?latex=g%3A%5B-b%2C-a%5D%5Cto%5Cmathbf+R&bg=ffffff&fg=333A42&s=0&c=20201002) be defined by
be defined by  . Show that
. Show that 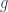 is also Riemann integrable, and
is also Riemann integrable, and ![\int_{[-b,-a]}g=\int_{[a,b]}f](https://s0.wp.com/latex.php?latex=%5Cint_%7B%5B-b%2C-a%5D%7Dg%3D%5Cint_%7B%5Ba%2Cb%5D%7Df&bg=ffffff&fg=333A42&s=0&c=20201002) .
.
Solution: For  , we can find a partition of
, we can find a partition of ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , namely
, namely  , and piecewise constant function
, and piecewise constant function  which majorizes
which majorizes  and
and  which minorizes
which minorizes  , both with respect to
, both with respect to  , such that
, such that
![\displaystyle{\int_{[a,b]}f-{\varepsilon}<\int_{[a,b]}\underline{f}\leq \int_{[a,b]}\overline{f}<\int_{[a,b]}f+{\varepsilon}}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%7B%5Cint_%7B%5Ba%2Cb%5D%7Df-%7B%5Cvarepsilon%7D%3C%5Cint_%7B%5Ba%2Cb%5D%7D%5Cunderline%7Bf%7D%5Cleq+%5Cint_%7B%5Ba%2Cb%5D%7D%5Coverline%7Bf%7D%3C%5Cint_%7B%5Ba%2Cb%5D%7Df%2B%7B%5Cvarepsilon%7D%7D&bg=ffffff&fg=333A42&s=0&c=20201002)
Now we define  and
and  on
on ![[-b,-a]](https://s0.wp.com/latex.php?latex=%5B-b%2C-a%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , then it is easy to see that
, then it is easy to see that  majorizes
majorizes 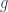 and
and  minorizes
minorizes 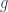 . For any
. For any  , we define
, we define  , then
, then  , and
, and  is a partition of
is a partition of ![[-b,-a]](https://s0.wp.com/latex.php?latex=%5B-b%2C-a%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , and the constant value of
, and the constant value of  on
on  is the same as the constant value of
is the same as the constant value of  on
on 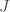 , the constant value of
, the constant value of  on
on  is the same as the constant value of
is the same as the constant value of  on
on 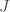 , so we have
, so we have
![\displaystyle{\int_{[-b,-a]}\overline{g}=p.c.\int_{[-b,-a]}\overline{g}=\sum_{K_J\in \mathbf P'}c_J |K_J|=\sum_{J\in \mathbf P}c_J |J| =\int_{[a,b]}\overline{f}}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%7B%5Cint_%7B%5B-b%2C-a%5D%7D%5Coverline%7Bg%7D%3Dp.c.%5Cint_%7B%5B-b%2C-a%5D%7D%5Coverline%7Bg%7D%3D%5Csum_%7BK_J%5Cin+%5Cmathbf+P%27%7Dc_J+%7CK_J%7C%3D%5Csum_%7BJ%5Cin+%5Cmathbf+P%7Dc_J+%7CJ%7C+%3D%5Cint_%7B%5Ba%2Cb%5D%7D%5Coverline%7Bf%7D%7D&bg=ffffff&fg=333A42&s=0&c=20201002)
Similarly we have
![\displaystyle{\int_{[-b,-a]}\underline{g}=\int_{[a,b]}\underline{f}}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%7B%5Cint_%7B%5B-b%2C-a%5D%7D%5Cunderline%7Bg%7D%3D%5Cint_%7B%5Ba%2Cb%5D%7D%5Cunderline%7Bf%7D%7D&bg=ffffff&fg=333A42&s=0&c=20201002)
So we have
![\displaystyle{\int_{[a,b]}f-{\varepsilon}<\int_{[-b,-a]}\underline{g}\leq \underline{\int}_{[-b,-a]}g\leq \overline{\int}_{[-b,-a]}g\leq \int_{[-b,-a]}\overline{g}<\int_{[a,b]}f+{\varepsilon}}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%7B%5Cint_%7B%5Ba%2Cb%5D%7Df-%7B%5Cvarepsilon%7D%3C%5Cint_%7B%5B-b%2C-a%5D%7D%5Cunderline%7Bg%7D%5Cleq+%5Cunderline%7B%5Cint%7D_%7B%5B-b%2C-a%5D%7Dg%5Cleq+%5Coverline%7B%5Cint%7D_%7B%5B-b%2C-a%5D%7Dg%5Cleq+%5Cint_%7B%5B-b%2C-a%5D%7D%5Coverline%7Bg%7D%3C%5Cint_%7B%5Ba%2Cb%5D%7Df%2B%7B%5Cvarepsilon%7D%7D&bg=ffffff&fg=333A42&s=0&c=20201002)
and the conclusion follows.

Exercise 11.10.4. What is the analogue of Proposition 11.10.7 when  is monotone decreasing instead of monotone increasing?
is monotone decreasing instead of monotone increasing?
Solution: Let ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=333A42&s=0&c=20201002) be a closed interval, and let
be a closed interval, and let ![{\phi}:[a,b]\to [{\phi}(b),{\phi}(a)]](https://s0.wp.com/latex.php?latex=%7B%5Cphi%7D%3A%5Ba%2Cb%5D%5Cto+%5B%7B%5Cphi%7D%28b%29%2C%7B%5Cphi%7D%28a%29%5D&bg=ffffff&fg=333A42&s=0&c=20201002) be a differentiable monotone decreasing function such that
be a differentiable monotone decreasing function such that  is Riemann integrable. Let
is Riemann integrable. Let ![f: [{\phi}(b),{\phi}(a)]\to \mathbf R](https://s0.wp.com/latex.php?latex=f%3A+%5B%7B%5Cphi%7D%28b%29%2C%7B%5Cphi%7D%28a%29%5D%5Cto+%5Cmathbf+R&bg=ffffff&fg=333A42&s=0&c=20201002) be a Riemann integrable function on
be a Riemann integrable function on ![[{\phi}(b),{\phi}(a)]](https://s0.wp.com/latex.php?latex=%5B%7B%5Cphi%7D%28b%29%2C%7B%5Cphi%7D%28a%29%5D&bg=ffffff&fg=333A42&s=0&c=20201002) . Then
. Then ![(f\circ {\phi}) {\phi}':[a,b]\to \mathbf R](https://s0.wp.com/latex.php?latex=%28f%5Ccirc+%7B%5Cphi%7D%29+%7B%5Cphi%7D%27%3A%5Ba%2Cb%5D%5Cto+%5Cmathbf+R&bg=ffffff&fg=333A42&s=0&c=20201002) is Riemann integrable on
is Riemann integrable on ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=333A42&s=0&c=20201002) and
and
![\displaystyle{\int_{[a,b]}(f\circ {\phi}) {\phi}'=-\int_{[{\phi}(b),{\phi}(a)]}f}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%7B%5Cint_%7B%5Ba%2Cb%5D%7D%28f%5Ccirc+%7B%5Cphi%7D%29+%7B%5Cphi%7D%27%3D-%5Cint_%7B%5B%7B%5Cphi%7D%28b%29%2C%7B%5Cphi%7D%28a%29%5D%7Df%7D&bg=ffffff&fg=333A42&s=0&c=20201002)

收敛的序列例子(1.1.17);最后是几个有用的结论:三种度量的等价性(1.1.18),离散空间的收敛实质是最终恒等于某一个点(1.1.19),极限是唯一的(1.1.20),当然极限的唯一性只在Hausdorff空间中成立;(1.1.21)说明使用不同的metric,收敛的点会不一样。




