这一节讲单调函数,虽然也很短,但单调函数性质很好,易应用,给出的两个例子一个是反函数的存在性(在讲反函数微分时会用到),另一个是构建n次方根的alternative method。习题不错
Exercise 9.8.1. Explain why the maximum principle remains true if the hypothesis that  is continuous is replaced with
is continuous is replaced with  being monotone, or with
being monotone, or with  being strictly monotone.
being strictly monotone.
Solution: If  and
and ![f:[a,b]\to \mathbf R](https://s0.wp.com/latex.php?latex=f%3A%5Ba%2Cb%5D%5Cto+%5Cmathbf+R&bg=ffffff&fg=333A42&s=0&c=20201002) is a monotonic function on
is a monotonic function on ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , then suppose first
, then suppose first  is monotonic increasing, we have
is monotonic increasing, we have ![f(b)\geq f(x),\forall x\in [a,b]](https://s0.wp.com/latex.php?latex=f%28b%29%5Cgeq+f%28x%29%2C%5Cforall+x%5Cin+%5Ba%2Cb%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , and
, and ![f(a)\leq f(x),\forall x\in [a,b]](https://s0.wp.com/latex.php?latex=f%28a%29%5Cleq+f%28x%29%2C%5Cforall+x%5Cin+%5Ba%2Cb%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , so
, so  attain its maximum at
attain its maximum at 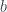 and its minimum at
and its minimum at  , if
, if  is strictly increasing, the proof is the same.
is strictly increasing, the proof is the same.
Suppose next that  is monotonic decreasing, we have
is monotonic decreasing, we have ![f(a)\geq f(x),\forall x\in [a,b]](https://s0.wp.com/latex.php?latex=f%28a%29%5Cgeq+f%28x%29%2C%5Cforall+x%5Cin+%5Ba%2Cb%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , and
, and ![f(b)\leq f(x),\forall x\in [a,b]](https://s0.wp.com/latex.php?latex=f%28b%29%5Cleq+f%28x%29%2C%5Cforall+x%5Cin+%5Ba%2Cb%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , so
, so  attain its maximum at a and its minimum at
attain its maximum at a and its minimum at 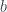 , if
, if  is strictly increasing, the proof is the same.
is strictly increasing, the proof is the same.

Exercise 9.8.2. Give an example to show that the intermediate value theorem becomes false if the hypothesis that  is continuous is replaced with
is continuous is replaced with  being monotone, or with
being monotone, or with  being strictly monotone.
being strictly monotone.
Solution: Let ![f:[-1,1]\to \mathbf R](https://s0.wp.com/latex.php?latex=f%3A%5B-1%2C1%5D%5Cto+%5Cmathbf+R&bg=ffffff&fg=333A42&s=0&c=20201002) be defined as:
be defined as:
![f(x)=\begin{cases}x,& x\in [-1,0)\\x+1,&x\in [0,1] \end{cases}](https://s0.wp.com/latex.php?latex=f%28x%29%3D%5Cbegin%7Bcases%7Dx%2C%26+x%5Cin+%5B-1%2C0%29%5C%5Cx%2B1%2C%26x%5Cin+%5B0%2C1%5D+%5Cend%7Bcases%7D&bg=ffffff&fg=333A42&s=0&c=20201002)
Then  is strictly monotone (thus monotone),
is strictly monotone (thus monotone),  and
and  , but no element in
, but no element in ![[-1,1]](https://s0.wp.com/latex.php?latex=%5B-1%2C1%5D&bg=ffffff&fg=333A42&s=0&c=20201002) could make
could make  .
.

Exercise 9.8.3. Let  be real numbers, and let
be real numbers, and let ![f:[a,b]\to\mathbf R](https://s0.wp.com/latex.php?latex=f%3A%5Ba%2Cb%5D%5Cto%5Cmathbf+R&bg=ffffff&fg=333A42&s=0&c=20201002) be a function which is both continuous and one-to-one. Show that
be a function which is both continuous and one-to-one. Show that  is strictly monotone.
is strictly monotone.
Solution: We shall divide into three cases:  . The first case is obviously a contradiction to
. The first case is obviously a contradiction to  is one-to-one. So we only consider the last two cases.
is one-to-one. So we only consider the last two cases.
Case  . Since
. Since  , then
, then  can be similarly proved. In this case
can be similarly proved. In this case  is strictly decreasing.
is strictly decreasing.
In conclusion  is strictly monotone.
is strictly monotone.

Exercise 9.8.4. Prove Proposition 9.8.3.Is the proposition still true if the continuity assumption is dropped, or if stricy monotonicity is replaced just by monotonicity? How should one modify the proposition to deal with strictly monotone decreasing functions instead of strictly monotone increasing functions?
Solution:  is strictly monotone increasing means
is strictly monotone increasing means  , and for
, and for ![\forall x,y\in [a,b],f(x)<f(y)](https://s0.wp.com/latex.php?latex=%5Cforall+x%2Cy%5Cin+%5Ba%2Cb%5D%2Cf%28x%29%3Cf%28y%29&bg=ffffff&fg=333A42&s=0&c=20201002) , thus
, thus  is injective. By the intermediate value theorem,
is injective. By the intermediate value theorem, ![\forall y\in [f(a),f(b)],\exists c\in [a,b],f(c)=y](https://s0.wp.com/latex.php?latex=%5Cforall+y%5Cin+%5Bf%28a%29%2Cf%28b%29%5D%2C%5Cexists+c%5Cin+%5Ba%2Cb%5D%2Cf%28c%29%3Dy&bg=ffffff&fg=333A42&s=0&c=20201002) , thus
, thus  is surjective. In conclusion
is surjective. In conclusion  is a bijection from
is a bijection from ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=333A42&s=0&c=20201002) to
to ![[f(a),f(b)]](https://s0.wp.com/latex.php?latex=%5Bf%28a%29%2Cf%28b%29%5D&bg=ffffff&fg=333A42&s=0&c=20201002) .
.
To prove  is continuous on
is continuous on ![[f(a),f(b)]](https://s0.wp.com/latex.php?latex=%5Bf%28a%29%2Cf%28b%29%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , choose some
, choose some ![y_0\in [f(a),f(b)]](https://s0.wp.com/latex.php?latex=y_0%5Cin+%5Bf%28a%29%2Cf%28b%29%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , then
, then ![\exists x_0\in [a,b],f(x_0 )=y_0](https://s0.wp.com/latex.php?latex=%5Cexists+x_0%5Cin+%5Ba%2Cb%5D%2Cf%28x_0+%29%3Dy_0&bg=ffffff&fg=333A42&s=0&c=20201002) . Now for
. Now for  , let
, let

Then as long as ![y\in [f(a),f(b)],|y-y_0 |<\delta](https://s0.wp.com/latex.php?latex=y%5Cin+%5Bf%28a%29%2Cf%28b%29%5D%2C%7Cy-y_0+%7C%3C%5Cdelta+&bg=ffffff&fg=333A42&s=0&c=20201002) , we can have
, we can have

Thus  is continuous.
is continuous.
To prove  is monotonic increasing on
is monotonic increasing on ![[f(a),f(b)]](https://s0.wp.com/latex.php?latex=%5Bf%28a%29%2Cf%28b%29%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , let
, let ![\forall y_1,y_2\in [f(a),f(b)],y_1<y_2](https://s0.wp.com/latex.php?latex=%5Cforall+y_1%2Cy_2%5Cin+%5Bf%28a%29%2Cf%28b%29%5D%2Cy_1%3Cy_2&bg=ffffff&fg=333A42&s=0&c=20201002) , then
, then ![\exists x_1,x_2\in [a,b]](https://s0.wp.com/latex.php?latex=%5Cexists+x_1%2Cx_2%5Cin+%5Ba%2Cb%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , s.t.
, s.t.  . Now we must have
. Now we must have  , otherwise contradicting
, otherwise contradicting  being strictly monotone increasing. This means
being strictly monotone increasing. This means  .
.
If the continuity assumption is dropped, the proposition is false, a counterexample may be
![f:[0,2]\to [0,3]:=\begin{cases}x,& x\in [0,1)\\x+1,& x\in [1,2] \end{cases}](https://s0.wp.com/latex.php?latex=f%3A%5B0%2C2%5D%5Cto+%5B0%2C3%5D%3A%3D%5Cbegin%7Bcases%7Dx%2C%26+x%5Cin+%5B0%2C1%29%5C%5Cx%2B1%2C%26+x%5Cin+%5B1%2C2%5D+%5Cend%7Bcases%7D&bg=ffffff&fg=333A42&s=0&c=20201002)
which is not a surjection to ![[0,3]](https://s0.wp.com/latex.php?latex=%5B0%2C3%5D&bg=ffffff&fg=333A42&s=0&c=20201002) . The inverse
. The inverse  exists but is not continuous.
exists but is not continuous.
If strict monotonicity is replaced by monotonicity, the proposition is false, a counterexample may be
![f:[0,2]\to \mathbf R:=1,\quad x\in [0,2]](https://s0.wp.com/latex.php?latex=f%3A%5B0%2C2%5D%5Cto+%5Cmathbf+R%3A%3D1%2C%5Cquad+x%5Cin+%5B0%2C2%5D&bg=ffffff&fg=333A42&s=0&c=20201002)
which is not an injection, and  doesn’t exist.
doesn’t exist.
To deal with strict monotone decreasing functions, we shall modify the proposition like this:
Let  be real numbers, and let
be real numbers, and let ![f:[a,b]\to \mathbf R](https://s0.wp.com/latex.php?latex=f%3A%5Ba%2Cb%5D%5Cto+%5Cmathbf+R&bg=ffffff&fg=333A42&s=0&c=20201002) be a function which is both continuous and strictly monotone decreasing. Then
be a function which is both continuous and strictly monotone decreasing. Then  is a bijection from
is a bijection from ![[a,b]](https://s0.wp.com/latex.php?latex=%5Ba%2Cb%5D&bg=ffffff&fg=333A42&s=0&c=20201002) to
to ![[f(b),f(a)]](https://s0.wp.com/latex.php?latex=%5Bf%28b%29%2Cf%28a%29%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , and the inverse
, and the inverse ![f^{-1}:[f(b),f(a)]\to [a,b]](https://s0.wp.com/latex.php?latex=f%5E%7B-1%7D%3A%5Bf%28b%29%2Cf%28a%29%5D%5Cto+%5Ba%2Cb%5D&bg=ffffff&fg=333A42&s=0&c=20201002) is also continuous and strictly monotone decreasing.
is also continuous and strictly monotone decreasing.

Exercise 9.8.5. In this exercise we give an example of a function which has a discontiuity at every rational point, but is continuous at every irrational. Since the rationals are countable, we can write them as  , where
, where  is a bijection from
is a bijection from  to
to  . Now define a function
. Now define a function  by setting
by setting  for each natrual number
for each natrual number  ; thus
; thus 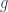 maps
maps  to
to 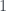 ,
,  to
to  , etc. Since
, etc. Since  is absolutely convergent, we see that
is absolutely convergent, we see that  is also absolutely convergent. Now define the function
is also absolutely convergent. Now define the function  by
by
 .
.
Since  is absolutely convergent, we know that
is absolutely convergent, we know that 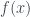 is well-defined for every real number
is well-defined for every real number  .
.
( a ) Show that  is strictly monotone increasing.
is strictly monotone increasing.
( b ) Show that for every rational number  ,
,  is discontinuous at
is discontinuous at  .
.
( c ) Show that for every irrational number  ,
,  is continuous at
is continuous at  .
.
Solution: ( a ) Given  , we can find
, we can find  , thus
, thus  , so
, so  . We have
. We have

( b )  . So given this
. So given this  , for
, for  :
:

By the comparison principle we have  , thus
, thus  , use Proposition 9.5.3 we can conclude
, use Proposition 9.5.3 we can conclude  is not continuous at
is not continuous at  .
.
( c ) First, we show  is continuous at irrational
is continuous at irrational  . Since there is at most
. Since there is at most  rationals
rationals  which could satisfy
which could satisfy  , we name them
, we name them  , then it is able to choose
, then it is able to choose

We conclude  remains constant for any
remains constant for any  , thus
, thus  is continuous at
is continuous at  . Also, notice that
. Also, notice that

Now for  , choose
, choose  s.t.
s.t.  , and for this
, and for this  choose
choose  s.t.
s.t.

Then if  , we can conclude
, we can conclude  , also
, also

So we can have

This proves  is continuous at
is continuous at  .
.

be a sequence of real numbers, then
can also be thought of as a function from
to
, which takes each natural number
to a real number
. Show that
, then
, s.t.
, then if
, we shall have
, this means
.
, then
, s.t.
in Definition 9.10.3, then we can see
.