这一节的逻辑构成是这样的:先定义了在countable集合上的级数,并且在绝对收敛下有Fubini定理成立,而后在uncountable集合上也可以定义级数,只要满足任何有限集合的sup存在。如果f是一个定义在uncountable集合上的绝对收敛级数,那么f非退化的点是至多可数的(证明需要用选择公理)。绝对收敛级数有很好理解的series laws,条件收敛级数则有Riemann的结论:可以收敛到任何实数L。这一节的习题主要是完善正文中的定理证明,然而也不易。
Exercise 8.2.1. Prove Lemma 8.2.3.
Lemma 8.2.3. Let  be an at most countable set, and let
be an at most countable set, and let  be a function. Then the series
be a function. Then the series  is absolutely convergent if and only if
is absolutely convergent if and only if

Solution: Exercise 3.6.3 says if there’s a function whose domain is on a finite subset of  , then the range of this function is also finite. I’ll use this result later.
, then the range of this function is also finite. I’ll use this result later.
Since  is at most countable,
is at most countable,  may be finite or countable. If
may be finite or countable. If  is finite, then the statement is obviously true. Now we consider the case when
is finite, then the statement is obviously true. Now we consider the case when  is countable.
is countable.
First suppose the series  is absolutely convergent, then there’s a bijection
is absolutely convergent, then there’s a bijection  such that
such that  is absolutely convergent. Given any element
is absolutely convergent. Given any element 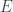 in the set
in the set

We know there’s a finite set  such that
such that  . So we can have a finite subset
. So we can have a finite subset  of
of 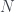 such that
such that  , from Exercise 3.6.3 we can have
, from Exercise 3.6.3 we can have  is bounded above by some natural number
is bounded above by some natural number 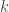 , so
, so

Since this is true for all 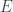 , we know that
, we know that  is an upper bound of
is an upper bound of 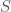 , so
, so

On the contrary, if  , we assume the series
, we assume the series  is not absolutely convergent, then given a bijection
is not absolutely convergent, then given a bijection  , we have
, we have  is not bounded above, so there exists a
is not bounded above, so there exists a  such that
such that  , we let
, we let  , then
, then  is finite, and
is finite, and

This leads to a contradiction.

Exercise 8.2.2. Prove Lemma 8.2.5.
Lemma 8.2.5. Let  be a set (which could be uncountable), and let
be a set (which could be uncountable), and let  be a function such that the series
be a function such that the series  is absolutely convergent. Then the set
is absolutely convergent. Then the set  is at most countable.
is at most countable.
Solution: Since  is absolutely convergent, the quantity
is absolutely convergent, the quantity

is well defined. For  , consider the set
, consider the set  , this set is finite with cardinality at most
, this set is finite with cardinality at most  , thus use Exercise 8.1.9, we know that
, thus use Exercise 8.1.9, we know that

is at most countable.

Exercise 8.2.3. Prove Proposition 8.2.6.
Solution: Since both  and
and  are absolutely convergent, the sets
are absolutely convergent, the sets  and
and  are at most countable. We denote
are at most countable. We denote  and
and  .
.
( a )  is absolutely convergent and
is absolutely convergent and

Solution: Let  be a finite set, then by proposition 7.1.11 we have
be a finite set, then by proposition 7.1.11 we have

which means

Use Definition 8.2.4 we know that  is absolutely convergent. Thus
is absolutely convergent. Thus

 is at most countable, if
is at most countable, if  is finite we can use Proposition 7.1.11(f) to get
is finite we can use Proposition 7.1.11(f) to get

If  is countable, we can have a bijection
is countable, we can have a bijection  , s.t.
, s.t.

Let  , we know that when
, we know that when  ,
,  since
since  , by the same logic,
, by the same logic,  , thus the conclusion is valid.
, thus the conclusion is valid.
( b ) If  is a real number, then
is a real number, then  is absolutely convergent, and
is absolutely convergent, and

Solution: If  the conclusion is obviously true. Now suppose
the conclusion is obviously true. Now suppose  , Let
, Let  be a finite set, then by proposition 7.1.11 we have
be a finite set, then by proposition 7.1.11 we have

Thus

Use Definition 8.2.4 we know that  is absolutely convergent. Since we also have
is absolutely convergent. Since we also have  , we know that
, we know that

If 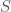 is finite, use Proposition 7.1.11(g) we have
is finite, use Proposition 7.1.11(g) we have  . If
. If 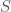 is countable, we can have a bijection
is countable, we can have a bijection  , s.t.
, s.t.

The last equality comes from Proposition 7.2.14(b).
( c ) If  for some disjoint sets $X_1$ and $X_2$, then
for some disjoint sets $X_1$ and $X_2$, then  and
and  are absolutely convergent, and
are absolutely convergent, and

Conversely, if  is such that
is such that  and
and  are absolutely convergent, then
are absolutely convergent, then  is also absolutely convergent, and
is also absolutely convergent, and

In the first case, let  be any finite set, then
be any finite set, then  , thus
, thus

Which gives

So  is absolutely convergent.
is absolutely convergent.
By the same logic  is absolutely convergent.
is absolutely convergent.
Conversely, if  and
and  are absolutely convergent. Then for any finite set
are absolutely convergent. Then for any finite set  , we can have
, we can have  , as
, as  and
and  are disjoint, we have
are disjoint, we have

Then we have

To prove  , we only need to consider points where
, we only need to consider points where  doesn’t vanish on, thus redefine
doesn’t vanish on, thus redefine

we first see the case is clear when  is finite. Now if one is countable and the other is finite, we may assume
is finite. Now if one is countable and the other is finite, we may assume  is finite, then there’s bijections
is finite, then there’s bijections  and
and  , such that
, such that

We define a bijection  by
by

Then  , further we have for any
, further we have for any  :
:

Let  , we get the conclusion.
, we get the conclusion.
If both sets are countable, there’s bijections  and
and  such that
such that

We define a bijection  by
by

Then  , further we have for any
, further we have for any  :
:

Let  , we get the conclusion.
, we get the conclusion.
The statement of  can then be derived by substituting
can then be derived by substituting  to
to 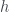 .
.
( d ) If 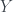 is another set, and
is another set, and  is a bijection, then
is a bijection, then  is absolutely convergent, and
is absolutely convergent, and

Solution: First we prove  is absolutely convergent. Choose any finite
is absolutely convergent. Choose any finite  , as
, as  is a bijection,
is a bijection,  is finite. Let
is finite. Let

Then  , so
, so

Next, to prove  , we see that for any
, we see that for any  such that
such that  , we can choose one
, we can choose one  such that
such that  , vice versa.(In this step we use the Axiom of Choice if
, vice versa.(In this step we use the Axiom of Choice if 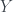 and
and  are uncountable) Thus the sets
are uncountable) Thus the sets  and
and  have the same cardinality, thus are both finite or countable. In the finite case the statement is obviously true by Proposition 7.1.11( c ). If both sets are countable, we let a bijection
have the same cardinality, thus are both finite or countable. In the finite case the statement is obviously true by Proposition 7.1.11( c ). If both sets are countable, we let a bijection  , then
, then  is also a bijection, and we have
is also a bijection, and we have

Then we have  .
.

Exercise 8.2.4. Prove Lemma 8.2.7.
Lemma 8.2.7. Let  be a series of real numbers which is conditionally convergent, but not absolutely convergent. Define the sets
be a series of real numbers which is conditionally convergent, but not absolutely convergent. Define the sets  and
and  , thus
, thus  and
and  . Then both of the series
. Then both of the series  and
and  are not conditionally convergent (and thus not absolutely convergent).
are not conditionally convergent (and thus not absolutely convergent).
Solution: Let  , we also know that
, we also know that  doesn’t exist. Now assume the conclusion is wrong, then one of the three assertions below must be true:
doesn’t exist. Now assume the conclusion is wrong, then one of the three assertions below must be true:
- i.
 converges, but
converges, but  is not conditionally convergent.
is not conditionally convergent. - ii.
 converges, but
converges, but  is not conditionally convergent.
is not conditionally convergent. - iii. both
 and
and  converges.
converges.
In case i and ii, we know that  , so we can have
, so we can have  in case i and
in case i and  in case ii, both are contradiction since the left side is not convergent but the right side is convergent.
in case ii, both are contradiction since the left side is not convergent but the right side is convergent.
In case iii, we let  and
and  , thus we have:
, thus we have:

which is a contradiction to the fact that  doesn’t exist. Thus the original conclusion must be true.
doesn’t exist. Thus the original conclusion must be true.

Exercise 8.2.5. Explain the gaps marked (why?) in the proof of Theorem 8.2.8.
Solution:
Why1:  and
and  are infinite.
are infinite.
Assume not, then one of  and
and  are finite, then either
are finite, then either  or
or  is a finite series, thus must be convergent, a contradiction.
is a finite series, thus must be convergent, a contradiction.
Why2:  and
and  are not absolutely convergent.
are not absolutely convergent.
Since  and
and  , if we assume
, if we assume  or
or  is absolutely convergent, then we can know from Proposition 7.4.3 that
is absolutely convergent, then we can know from Proposition 7.4.3 that  or
or  , in particular either
, in particular either  or
or  is absolute convergent, which is a contradiction.
is absolute convergent, which is a contradiction.
Why3: The map  is injective.
is injective.
Let  , then either
, then either  or
or  , if
, if  , the definition of
, the definition of  guarantees that
guarantees that  . If
. If  we can similarly prove
we can similarly prove  , so this map is injective.
, so this map is injective.
Why4: Both Case I and II occur an infinite number of times.
Assume Case I only occurs finite number of times, this means for some  , we’ll have
, we’ll have

Thus we have  , or
, or  , notice that as
, notice that as 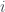 increases,
increases,  decreases since all
decreases since all  , so
, so  converges, which means
converges, which means  converges, a contradiction.
converges, a contradiction.
When assume Case II occurs finite number of times, we can prove a contradiction similarly.
Why5: The map  is surjective.
is surjective.
For  , either
, either  or
or  . Assume no
. Assume no  can make
can make  , this means either Case I or Case II stops at
, this means either Case I or Case II stops at  , so can only occur finite number of times, which is a contradiction.
, so can only occur finite number of times, which is a contradiction.
Why6: 
From Corollary 7.2.6 we have  , since both Case I and II occur an infinite number of times, when
, since both Case I and II occur an infinite number of times, when  we must have
we must have  .
.
Why7: 
From Why6 we know that for  ,s.t.
,s.t. . Start from
. Start from  , we search for a number
, we search for a number  such that
such that  and
and  , this
, this 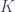 must exist, otherwise we’ll get a contradiction with Why4.
must exist, otherwise we’ll get a contradiction with Why4.
We denote  , notice that:
, notice that:
If  , we shall add positive
, we shall add positive  to
to  , the positive adding shall stop once
, the positive adding shall stop once  , so
, so  , if
, if  , we can have
, we can have  .
.
If  , we shall add negative
, we shall add negative  to
to  , the negative adding shall stop once
, the negative adding shall stop once  , so
, so  , if
, if  , we can have
, we can have  .
.
Combined we get  , this means
, this means  .
.

Exercise 8.2.6. Let  be a series which is conditionally convergent, but not absolutely convergent. Show that there exists a bijection
be a series which is conditionally convergent, but not absolutely convergent. Show that there exists a bijection  such that
such that  diverges to
diverges to  , or more precisely that
, or more precisely that
 .
.
Of course, a similar statement holds with  replaced by
replaced by  .
.
Solution: We only have to prove  . With the same definition of
. With the same definition of  and
and  in Lemma 8.2.7, we find increasing bijections
in Lemma 8.2.7, we find increasing bijections  and
and  . We define a sequence
. We define a sequence  of natural numbers recursively as below:
of natural numbers recursively as below:
Let  . Suppose that
. Suppose that  is a natural number, and
is a natural number, and 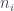 has already be defined for all
has already be defined for all  . Then we let
. Then we let

For example, if  , then
, then  and
and  has been defined, then
has been defined, then  . Now
. Now
(I) If  , we set
, we set 
(II) If  , we set
, we set 
Intuitively, we compare  with an increasing
with an increasing 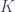 , which increases by
, which increases by 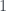 once we add an negative number to the sum. From the proof of Exercise 8.2.5 we can see that
once we add an negative number to the sum. From the proof of Exercise 8.2.5 we can see that
 and
and  are infinite.
are infinite. and
and  are not absolutely convergent.
are not absolutely convergent.- The map
 is injective.
is injective.
And we can prove the following results:
- Both Case I and II occur an infinite number of times.
Assume Case I occur only finite number of times, then from some 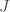 and
and 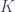 we’ll get
we’ll get  and Case II happens infinitely, but as we add negative numbers to
and Case II happens infinitely, but as we add negative numbers to  , we’ll have
, we’ll have  , and
, and  , this will lead to a contradiction since
, this will lead to a contradiction since  is finite.
is finite.
Assume Case II occur only finite number of times, then from some 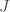 and
and 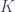 we’ll get
we’ll get  , and
, and  , this means
, this means  is convergent, a contradiction.
is convergent, a contradiction.
- The map
 is surjective.
is surjective.  .
.
The proofs are similar to that of Exercise 8.2.5.
Finally we shall prove  for any
for any  , thus complete the proof. For any
, thus complete the proof. For any  , we can find a natural number
, we can find a natural number  , and as
, and as  , there’s
, there’s 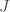 such that
such that

We’ll eventually find a  such that
such that  , and adding negative
, and adding negative  to the sum would not let the new sum falls below
to the sum would not let the new sum falls below 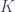 , once the sum is between
, once the sum is between 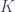 and
and  , we would continue to add positive
, we would continue to add positive  and push the sum to
and push the sum to  and even larger, thus we have
and even larger, thus we have  , and the conclusion follows.
, and the conclusion follows.

be a finite set of cardinality
. Show that
is a finite set of cardinality
.
then
and the only element in
is
, so the cardinality of
is
.
, let
be a finite set of cardinality
, since
, so choose
, then set
has cardinality
, and
has cardinality
. For any set
,
is a subset of
which contains
. Thus we can see that
equals the cardinality of
, then we have
has cardinality
. Finally, from
and
we have
be sets such that
, and suppose that there is a injection
. Define the sets
recursively by setting
, and then
for all natural numbers
. Prove that the sets
are all disjoint from each other (i.e.,
whenever
). Also show that if
is the function defined by setting
when
, and
when
, then
does indeed map
to
and is a bijection between the two. In particular,
and
have the same cardinality.
, if we assume there’s
, we can safely assume
, then
, s.t.
times we would get
, which is a contradiction.
is defined as above, notice that
, and if
, we shall have
, if
we have
. So g does map
to
.
is a bijection:
, if
we directly get
. If
we have
, thus
and
is impossible, assume so, then
, and
, so we have
, since
, we can’t have
, then
, which is a contradiction. The case that
and
is impossible by the same logic. So we finished proving g is an injection.
, we must have one and only one of the two cases valid:
, then let
, we have
.
, we must have
since
, we let
, then
. We finished proving
is a surjection.
is said to have lesser or equal cardinality than a set
iff there is an injective map
from
to
. Using Exercise 8.3.2, show that if
are sets such that
has lesser or equal cardinality to
and
has lesser or equal cardinality to
, then
and
have equal cardinality. (This is known as the Schröder-Bernstein theorem.)
and
be injections, we can have
and
, thus
. We can see that
is an bijection from
to
. Let
are disjoint from each other. Let
be defined by setting
if
, and
if
, then due to Exercise 8.3.2,
is a bijection, so
.
has strictly lesser cardinality than a set
if
has lesser or equal cardinality to
, but
does not have equal cardinality to
. Show that for any set
, that
has strictly lesser cardinality than
. Also, show that if
has strictly lesser cardinality than
, and
has strictly lesser cardinality than
, then
has strictly lesser cardinality than
.
by
, thus
has lesser than or equal cardinality to
, and due to Theorem 8.3.1,
doesn’t have equal cardinality to
.
and
, thus
is an injection, thus
, now suppose
has equal cardinality to
, then
, combined with
we get
from Exercise 8.3.3, this is a contradiction since
has strictly lesser cardinality than
.
for some set
) can be countably infinite.
is finite, then from Exercise 8.3.1 we know that
is finite.
is countable, then
, from Cantor’s Theorem we know that
, so
is uncountable.
is uncountable, then
, so
is uncountable.