先建立了有限级数的各种性质(本质是部分和的性质),这样无限级数可以当作部分和的极限处理,就可以利用原来关于数列极限的各项结论。同时还建立了对有限集合上求和的概念,后续可以拓展到可数集合上。最后是一个很有用的结论即Fubini定理,有限级数的求和可以换序。
Exercise 7.1.1. Prove Lemma 7.1.4.
Solution:
( a ) For any  we use induction on
we use induction on 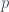 :
:
For  , we know that in this case
, we know that in this case  can only be
can only be 

Now suppose for 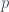 the statement holds, then for
the statement holds, then for  : for all
: for all  we have
we have

And for  :
:

Thus the conclusion holds.
( b ) Given  we use induction on
we use induction on  :
:
For  , we have
, we have

Now suppose for  the statement holds, then for
the statement holds, then for  , we have
, we have

Thus the conclusion holds.
( c ) Given  we use induction on
we use induction on  :
:
For  , we have
, we have

Now suppose for  the statement holds, then for
the statement holds, then for  , we have
, we have

Thus the conclusion holds.
( d ) Given  we use induction on
we use induction on  :
:
For  , we have
, we have

Now suppose for  the statement holds, then for
the statement holds, then for  , we have
, we have

Thus the conclusion holds.
( e ) Given  we use induction on
we use induction on  :
:
For  , we have
, we have

Now suppose for  the statement holds, then for
the statement holds, then for  , we have
, we have

Thus the conclusion holds.
( f ) Given  we use induction on
we use induction on  :
:
For  , we have
, we have

Now suppose for  the statement holds, then for
the statement holds, then for  , we have
, we have

Thus the conclusion holds.

Exercise 7.1.2. Prove Proposition 7.1.11.
Solution:
( a ) We assign a function  , then
, then 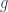 is a bijection, so
is a bijection, so

( b ) We assign a function  by
by  , then
, then 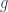 is a bijection, so
is a bijection, so

( c ) Suppose  has
has  elements, then
elements, then 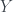 must have
must have  elements. We assign a bijective function
elements. We assign a bijective function  , then the function
, then the function  is a bijection, thus we have
is a bijection, thus we have

On the other hand, 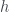 is a bijection means given the function
is a bijection means given the function 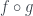 , we have
, we have

( d ) We use the bijection  to be
to be  , then
, then

( e ) Suppose  has
has  elements and
elements and 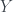 has
has  elements, then we can find bijections:
elements, then we can find bijections:

So we can have

Now we define  as follows:
as follows:

It’s easy to see that 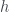 is a bijection, so use Lemma 7.1.4 (a) and (b) we have
is a bijection, so use Lemma 7.1.4 (a) and (b) we have

( f ) Suppose  has
has  elements, we assign a bijection
elements, we assign a bijection  , so
, so

( g ) Suppose  has
has  elements, we assign a bijection
elements, we assign a bijection  . So by Lemma 7.1.4(d)
. So by Lemma 7.1.4(d)

( h ) Suppose  has
has  elements, we assign a bijection
elements, we assign a bijection  , so
, so

Which means by Lemma 7.1.4(f)

( i ) Suppose  has
has  elements, we assign a bijection
elements, we assign a bijection  .
.
So by Lemma 7.1.4(e)


Exercise 7.1.3. Form a definition for the finite products  and
and  . Which of the above results for finite series have analogues for finite products?
. Which of the above results for finite series have analogues for finite products?
Solution:
(Finite products). Let  be integers, and let
be integers, and let  be a finite sequence of real numbers, assigning a real number
be a finite sequence of real numbers, assigning a real number  to each integer
to each integer 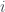 between
between  and
and  inclusive. Then we define the finite product
inclusive. Then we define the finite product  by the recursive formula
by the recursive formula

(Production over finite sets). Let  be a finite set with
be a finite set with  elements
elements  , and let
, and let  . Then we can select any bijection
. Then we can select any bijection  , we then define
, we then define

We have Lemma 7.1.4’:
( a ) 
( b ) 
( c ) 
( d ) 
( e ) 
Also Lemma 7.1.11 is valid through (a)-(g) and (i) with summation replaced by products.

Exercise 7.1.4. Define the factorial function  for natural numbers
for natural numbers  by the recursive definition
by the recursive definition  and
and  . If
. If  and
and  are real numbers, prove the binomial formula
are real numbers, prove the binomial formula

for all natural numbers  .
.
Solution: We induct on  :
:
When  , we have
, we have

Now suppose the case is true for  , consider
, consider  :
:
\\&=\sum_{j=0}^n\dfrac{n!}{j!(n-j)!} x^{j+1} y^{n-j}+\sum_{j=0}^n\dfrac{n!}{j!(n-j)!} x^j y^{n+1-j}\\&=\sum_{j=0}^{n-1}\dfrac{n!}{j!(n-j)!} x^{j+1} y^{n-j}+x^{n+1}+y^{n+1}+\sum_{j=1}^n\dfrac{n!}{j!(n-j)!} x^j y^{n+1-j}\\&=x^{n+1}+y^{n+1}+\sum_{j=1}^n\dfrac{n!}{(j-1)!(n-j+1)!} x^j y^{n-j+1}+\sum_{j=1}^n\dfrac{n!}{j!(n-j)!} x^j y^{n+1-j}\end{aligned}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Baligned%7D%28x%2By%29%5E%7Bn%2B1%7D%26%3D%28x%2By%29%5En+%28x%2By%29%3D%5Cleft%5B%5Csum_%7Bj%3D0%7D%5En%5Cdfrac%7Bn%21%7D%7Bj%21%28n-j%29%21%7D+x%5Ej+y%5E%7Bn-j%7D%5Cright%5D%28x%2By%29%5C%5C%26%3D%5Csum_%7Bj%3D0%7D%5En%5Cdfrac%7Bn%21%7D%7Bj%21%28n-j%29%21%7D+x%5E%7Bj%2B1%7D+y%5E%7Bn-j%7D%2B%5Csum_%7Bj%3D0%7D%5En%5Cdfrac%7Bn%21%7D%7Bj%21%28n-j%29%21%7D+x%5Ej+y%5E%7Bn%2B1-j%7D%5C%5C%26%3D%5Csum_%7Bj%3D0%7D%5E%7Bn-1%7D%5Cdfrac%7Bn%21%7D%7Bj%21%28n-j%29%21%7D+x%5E%7Bj%2B1%7D+y%5E%7Bn-j%7D%2Bx%5E%7Bn%2B1%7D%2By%5E%7Bn%2B1%7D%2B%5Csum_%7Bj%3D1%7D%5En%5Cdfrac%7Bn%21%7D%7Bj%21%28n-j%29%21%7D+x%5Ej+y%5E%7Bn%2B1-j%7D%5C%5C%26%3Dx%5E%7Bn%2B1%7D%2By%5E%7Bn%2B1%7D%2B%5Csum_%7Bj%3D1%7D%5En%5Cdfrac%7Bn%21%7D%7B%28j-1%29%21%28n-j%2B1%29%21%7D+x%5Ej+y%5E%7Bn-j%2B1%7D%2B%5Csum_%7Bj%3D1%7D%5En%5Cdfrac%7Bn%21%7D%7Bj%21%28n-j%29%21%7D+x%5Ej+y%5E%7Bn%2B1-j%7D%5Cend%7Baligned%7D&bg=ffffff&fg=333A42&s=0&c=20201002)
We have

So the expression equals to

Thus the conclusion holds.

Exercise 7.1.5. Let  be a finite set, let
be a finite set, let  be an integer, and for each
be an integer, and for each  let
let  be a convergent sequence of real numbers. Show that the sequence
be a convergent sequence of real numbers. Show that the sequence  is convergent, and
is convergent, and
 .
.
Solution: Suppose  has
has  elements, we induct on
elements, we induct on  .
.
If  , then
, then  , since
, since  and
and  are both functions, use Proposition 7.1.11(a) we know that the left side equals
are both functions, use Proposition 7.1.11(a) we know that the left side equals  , and the right side is
, and the right side is 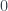 .
.
Now suppose the statement is true for  consider
consider  . As
. As  , we can choose
, we can choose  , and
, and  is a convergent sequence of real numbers. Let
is a convergent sequence of real numbers. Let  , then
, then 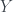 has
has  elements, so we have
elements, so we have

By the induction hypothesis  is convergent, thus
is convergent, thus  is convergent, and we have
is convergent, and we have


convergent or divergent? Justify your answer.
, then
if
is even,
if
is odd, thus the upper limit and lower limit of
does not equal.
, then
converges iff
converges, which is true iff
is a Cauchy sequence, i.e. for
such that
, then for each
, and every integer
, we can have a
such that
. Now if
converges, given an
, we can find an
such that
, we choose a
s.t.
, then if
, we shall have
is absolutely convergent, then
is convergent, thus by Proposition 7.2.5, for every
such that
is convergent. Now define
, so we know that
, then
, also we have
:
, we can have
we get the desired result.
, we know
, thus
, it’s easy to see that
, then