limsup和liminf是(至少我认为)比较难以理解的概念,不过这个概念和极限点limit points的联系是很直接的。这一节用先定义一个新的序列,再取序列上下确界的方法定义limsup和liminf,能让这个东西显得直观一些。6.4.12-6.4.15是比较重要的结论,后面的章节也会经常用到。这一节最后提到并证明了实数集的完备性。
Exercise 6.4.1. Prove Proposition 6.4.5.
Solution: For  , there’s
, there’s  s.t.
s.t. . So that for any
. So that for any  , we just need to choose
, we just need to choose  , then
, then  . This shows
. This shows  to be a limit point of
to be a limit point of  . To see that
. To see that  is the only limit point of
is the only limit point of  , we let
, we let  , then as
, then as  , for
, for  , there’s
, there’s  , such that
, such that

This means

So that  is not
is not  -adherent to
-adherent to  , which means
, which means  is not a limit point.
is not a limit point.

Exercise 6.4.2. State and prove analogue of Exercises 6.1.3 and 6.1.4 for limit points, limit superior, and limit inferior.
Solution:
Statement I:
Let  be a sequence of real numbers, let
be a sequence of real numbers, let  be a real number, and
be a real number, and  be an integer. Show that
be an integer. Show that  is a limit point of
is a limit point of  if and only if
if and only if  is a limit point of
is a limit point of  , and
, and  for
for  if and only if
if and only if  for
for  , and
, and  for
for  if and only if
if and only if  for
for  .
.
Proof:
For the limit point case:
 is a limit point of
is a limit point of  means
means  , this includes the case that
, this includes the case that  , which means
, which means  is a limit point of
is a limit point of  .
.
On the other hand,  means
means  , and once we find an
, and once we find an  when
when  , we can let this
, we can let this  be the element we need when
be the element we need when  .
.
For the limsup and liminf case:
By definition,  , where
, where  . As
. As  , we have
, we have

So that  . Now assume
. Now assume  , then
, then  such that
such that

So  is not a lower bound of
is not a lower bound of  , which means there’s
, which means there’s  , but obviously
, but obviously  , so
, so  is a contradiction. Thus we must have
is a contradiction. Thus we must have

The 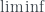 case can be similarly proved.
case can be similarly proved.
Statement II:
Let  be a sequence of real numbers, let
be a sequence of real numbers, let  be a real number, and
be a real number, and  be an non-negative integer. Show that
be an non-negative integer. Show that  is a limit point of
is a limit point of  if and only if
if and only if  is a limit point of
is a limit point of  , and
, and  for
for  if and only if
if and only if  for
for  , and
, and  for
for  if and only if
if and only if  for
for  .
.
Proof:
For the limit point case:
 is a limit point of
is a limit point of  means
means  , this includes the case that
, this includes the case that  , which means
, which means  is a limit point of
is a limit point of  .
.
On the other hand,  means
means  , and once we find an
, and once we find an  when
when  , we can let this
, we can let this  be the element we need when
be the element we need when  .
.
For the limsup and liminf case:
By definition,  , where
, where  . As
. As  , we have
, we have

So that  . Now assume
. Now assume  , then
, then  such that
such that

So  is not a lower bound of
is not a lower bound of  , which means there’s
, which means there’s 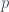 , s.t.
, s.t.  , but obviously
, but obviously  , so
, so  is a contradiction. Thus we must have
is a contradiction. Thus we must have

The 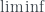 case can be similarly proved.
case can be similarly proved.

Exercise 6.4.3. Prove parts (c),(d),(e),(f) of Proposition 6.4.12.
Solution:
( c )  ,
, 
To prove  , we assume
, we assume  , then
, then  , by the definition of infimum, we can find an
, by the definition of infimum, we can find an  , again by the definition of supremum, we can find an
, again by the definition of supremum, we can find an  s.t.
s.t.  , now choose
, now choose  , then
, then  , so we get a contradiction from
, so we get a contradiction from

( d ) With the help of (c) we only need to show  and
and  . Assume
. Assume  , then let
, then let  , by the definition of
, by the definition of  we can have some
we can have some  such that
such that  , which means
, which means

This contradicts  to be a limit point of
to be a limit point of  . Thus
. Thus  . If
. If  we let $\varepsilon=1$ to complete the proof. Finally the case in which
we let $\varepsilon=1$ to complete the proof. Finally the case in which  can be similarly proved.
can be similarly proved.
( e )  and
and  , by ( a ) we can find
, by ( a ) we can find  such that
such that  for all
for all  , by ( b ) we can find
, by ( b ) we can find  such that
such that  . Then we have
. Then we have

which means  is a limit point of
is a limit point of  . The case of
. The case of  is proved similarly.
is proved similarly.
( f ) If  converges to
converges to  , then by (e), we have
, then by (e), we have  . Conversely if
. Conversely if  , then by (d) the limit point of
, then by (d) the limit point of  can only be
can only be  , thus
, thus  converges to
converges to  .
.

Exercise 6.4.4. Prove Lemma 6.4.13.
Solution: We have, for all  :
:

The above inequality is independent of the starting number  , thus we can have
, thus we can have

Again using the first two statements, we can get the remaining two statements.

Exercise 6.4.5. Use Lemma 6.4.13 to prove Corollary 6.4.14.
Solution: From  we can have
we can have  .
.
From  we can have
we can have  .
.
Together we have  , using Proposition 6.1.12 (f) we are done.
, using Proposition 6.1.12 (f) we are done.

Exercise 6.4.6. Give an example of two bounded sequences  and
and  such that
such that  for all
for all  , but that
, but that  . Explain why this does not contradict Lemma 6.4.13.
. Explain why this does not contradict Lemma 6.4.13.
Solution: We can have  and
and  for all
for all  , then obviously
, then obviously  , but
, but

Lemma 6.4.13 requires  not
not  , so this is not a violation.
, so this is not a violation.

Exercise 6.4.7. Prove Corollary 6.4.17. Is the corollary still true if we replace zero in the statement of this Corollary by some other number?
Solution: If  , then
, then  , by
, by  and squeeze test,
and squeeze test,  .
.
If  , then
, then  , there’s
, there’s  such that
such that

Which means  , thus
, thus  .
.
If we replace 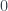 by other number the Corollary can be wrong.
by other number the Corollary can be wrong.

Exercise 6.4.8. Let us say that a sequence  of real numbers has
of real numbers has  as a limit point iff it has no finite upper bound, and that it has
as a limit point iff it has no finite upper bound, and that it has  as a limit point iff it has no finite lower bound. With this definition, show that
as a limit point iff it has no finite lower bound. With this definition, show that  is a limit point of
is a limit point of  , and futthermore that it is larger than all the other limit points of
, and futthermore that it is larger than all the other limit points of  ; in other words, the limit superior is the largest limit point of a sequence. Similarly, show that the limit inferior is the smallest limit point of a sequence.
; in other words, the limit superior is the largest limit point of a sequence. Similarly, show that the limit inferior is the smallest limit point of a sequence.
Solution: Given  , we know it may or may not have finite upper bound. If it does have, then
, we know it may or may not have finite upper bound. If it does have, then

Then by Proposition 6.4.12(e) we know  is a limit point of
is a limit point of  , and by Proposition 6.4.12(d) we know it’s larger than all other limit points of
, and by Proposition 6.4.12(d) we know it’s larger than all other limit points of  .
.
If it has no finite upper bound, then  is a limit point of
is a limit point of  by the condition given in the exercise, and if
by the condition given in the exercise, and if  is a limit point of
is a limit point of  , we must have
, we must have  .
.
The case of limit inferior can be proved similarly.

Exercise 6.4.9. Using the definition in Exercise 6.4.8, construct a sequence  which has exactly three limit points, at
which has exactly three limit points, at  and
and  .
.
Solution: The sequence  which is
which is


Exercise 6.4.10. Let  be a sequence of real numbers, and let
be a sequence of real numbers, and let  be another sequence of real numbers such that each
be another sequence of real numbers such that each  is a limit point of
is a limit point of  . Let
. Let  be a limit point of
be a limit point of  . Prove that
. Prove that  is also a limit point of
is also a limit point of  .
.
Solution: For  , there’s
, there’s  such that
such that  , for this
, for this  , which is a limit point of
, which is a limit point of  , there’s
, there’s  such that
such that  , so we have
, so we have

Which means  is a limit point of
is a limit point of  .
.

is a subsequence of
, we have
a strictly increasing function.
is a subsequence of
,
is a subsequence of
, then there’re two strictly increasing functions
such that
, then
is strictly increasing since
.
and
which are not the same sequence, but such that each is a subsequence of the other?
be a sequence which is not bounded. Show that there exists a subsequence
of
such that
exists and is equal to zero.
, and for every
, we recursively let
, the set
is empty, then for every
we have
, this means
is bounded by the number
, which is a contradiction to the fact that
is unbounded.
, we see that
, thus
.
is a subsequence of itself.
be a subsequence of
, then as
, for
there’s
s.t.
. Since
, we have
.
and for
:
is a limit point of
, for every
we can find a
such that
, so this set is never empty. Now the sequence
converges to
.
, there’s
s.t.
, but
is an item of
, so the conclusion follows.