这一节开始讲实际的极限,建立metric概念(其实是实直线上的标准度量)和极限算律,从这一章起,内容与普通实分析差异不大,但由于有第2-5章的基础,从这章开始的进度是明显加快的,其后只用6章就把单变量微积分的严格构建以及实数型级数介绍完毕,还附带说了一些集合论的东西(第8章),由此可以看出基础打得好的作用,如果前面做题扎实,从第6章开始读完Analysis I的感觉应该是基本上每个概念都很清晰。本章起习题有所增加,且相对常规化,但仍都值得一做。
Exercise 6.1.1. Let  be a sequence of real numbers, such that
be a sequence of real numbers, such that  for each natural number
for each natural number  . Prove that whenever
. Prove that whenever  and
and  are natural numbers such that
are natural numbers such that  , then we have
, then we have  . (We refer to these sequences as increasing sequences.)
. (We refer to these sequences as increasing sequences.)
Solution: Given  fixed and we induct on
fixed and we induct on  :
:
For  , we have
, we have  by condition given.
by condition given.
Suppose  and
and  , then for
, then for  , we have
, we have  , thus the induction hypothesis is valid.
, thus the induction hypothesis is valid.

Exercise 6.1.2. Let  be a sequence of real numbers, and let
be a sequence of real numbers, and let 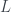 be a real number. Show that
be a real number. Show that  converges to
converges to 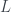 if and only if, given any
if and only if, given any  , one can find an
, one can find an  such that
such that  for all
for all  .
.
Solution:


Exercise 6.1.3. Let  be a sequence of real numbers, let
be a sequence of real numbers, let  be a real number, and let
be a real number, and let  be an integer. Show that
be an integer. Show that  converges to
converges to  if and only if
if and only if  converges to
converges to  .
.
Solution: Use Exercise 6.1.2 we have

The other direction is easy since any  we’ll have
we’ll have  .
.

Exercise 6.1.4. Let  be a sequence of real numbers, let
be a sequence of real numbers, let  be a real number, and let
be a real number, and let  be a non-negative integer. Show that
be a non-negative integer. Show that  converges to
converges to  if and only if
if and only if  converges to
converges to  . Solution:
. Solution:  converges to
converges to  means
means

Thus if  , then
, then  , thus
, thus  , so
, so  converges to
converges to  . Conversely, if
. Conversely, if  converges to
converges to  , then
, then

Let  , then if
, then if  we have
we have  , so
, so  converges to
converges to  .
.

Exercise 6.1.5. Prove Proposition 6.1.12.
Solution: For  , let
, let  , then
, then  , thus if
, thus if  ,
,

This means  is a Cauchy sequence.
is a Cauchy sequence.

Exercise 6.1.6. Prove Proposition 6.1.15.
Solution: We assume  is not eventually
is not eventually  -close to
-close to 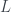 , then first there’s a
, then first there’s a  such that
such that

Next, we can find a  such that
such that

Let  , use both results we can have
, use both results we can have

This means for all  , either
, either  or
or  , by Exercise 5.4.8, we shall have
, by Exercise 5.4.8, we shall have  or
or  , both leads to a contradiction.
, both leads to a contradiction.

Exercise 6.1.7. Show that Definition 6.1.16 is consistent with Definition 5.1.12.
Solution: We have to show the following result is true:
Let  be a sequence of rational numbers starting at some integer index
be a sequence of rational numbers starting at some integer index  , then
, then  is bounded in the sense of Definition 6.1.16 iff
is bounded in the sense of Definition 6.1.16 iff  is bounded in the sense of Definition 5.1.12.
is bounded in the sense of Definition 5.1.12.
We first suppose  is bounded in the sense of Definition 6.1.16, i.e.
is bounded in the sense of Definition 6.1.16, i.e.  , s.t.
, s.t.

As  is a positive real, we can have a positive integer (thus rational)
is a positive real, we can have a positive integer (thus rational) 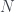 such that
such that  , so we can have
, so we can have

This shows that  is bounded in the sense of Definition 5.1.12.
is bounded in the sense of Definition 5.1.12.
On the other hand, suppose  is bounded in the sense of Definition 5.1.12. Then we can find a rational
is bounded in the sense of Definition 5.1.12. Then we can find a rational  such that
such that

Since  is also a real number, we get the result directly.
is also a real number, we get the result directly.

Exercise 6.1.8. Prove Theorem 6.1.19.
Solution: We let  : then have
: then have

Further, convergent sequences are bounded, so we have  , and
, and

( a ) The result comes from

( b ) We have, for all  :
:

( c ) Let  and use (b).
and use (b).
( d ) From (c) we can get

And then use (b) to get the result.
( e ) Since  , we know that there’s
, we know that there’s  such that
such that

Which means when 

As  , we show that
, we show that  is bounded away from
is bounded away from 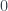 , so there’s
, so there’s 

Thus

( f ) We use the notation of  in (e), then
in (e), then

( g ) If  , then
, then  and
and  are equivalent Cauchy sequence, thus when
are equivalent Cauchy sequence, thus when  :
:

Which means

Now assume  , then there’s
, then there’s 

Which will lead to

So that  , using Exercise 6.1.3 we know that
, using Exercise 6.1.3 we know that

( h ) A similar proof like (g) can be made by the same logic.

Exercise 6.1.9. Explain why Theorem 6.1.19(f) fails when the limit of the denominator is 0.
Solution: Let  and
and  , then by Proposition 6.1.11:
, then by Proposition 6.1.11:

But  , so the expression
, so the expression  is meaningless.
is meaningless.

Exercise 6.1.10. Show that the concept of equivalent Cauchy sequence, as defined in Definition 5.2.6, does not change if  is required to be positive real instead of positive rational. More precisely, if
is required to be positive real instead of positive rational. More precisely, if  and
and  are sequences of reals, show that
are sequences of reals, show that  and
and  are eventually
are eventually  -close for every rational
-close for every rational  if and only if they are eventually
if and only if they are eventually  -close for every real
-close for every real  .
.
Solution: Eventually  -close for every real
-close for every real  implies eventually
implies eventually  -close for every rational
-close for every rational  .
.
To prove the converse, suppose  and
and  are eventually
are eventually  -close for every rational
-close for every rational  , then given any real
, then given any real 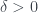 , we can have a rational
, we can have a rational  such that
such that  , and an integer
, and an integer 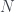 s.t.
s.t.

This means  and
and  are eventually
are eventually  -close.
-close.

, we first notice that
, also for any number
, since
, we have
, thus
is not an upper bound of
.
, we first see that
, also for any number
, by the Archimedean property we have a positive integer
such that
or
, this means
, so
is not an lower bound of
.
, then
by Definition 6.3.1, and by Theorem 6.2.11 (a), for all
we have
, thus
.
is an upper bound for
, then
is an upper bound for
, by Theorem 6.2.11 (b) we have
.
, then
, assume for all
we have
, then
is an upper bound of
, also
, so
, as
,
shall be no larger than
by definition, this is an contradiction.
, then
by Proposition 6.3.6. Let
, we have
, so
. In fact, show that the sequence
diverges when
.
, assume
converges to
, then we have
and
, we let
and get
, which is a contradiction.