城南讲马堂

陶哲轩实分析4.1及习题-Analysis I 4.1

2019年4月5日2019年12月13日christangdt留下评论

使用减法来从自然数定义整数是非常新颖的，当然这里是一种形式减法。不过自此对于很多整数的概念更好导出，比较重要的比如整数的三歧性，整数代数运算律，0的作用，消去律等，都容易证明；最后说了整数的排序。这一节和之后的自然数节，都是先定义，再提出一些等式性规律，再导出排序（不等式规律）。习题很有价值，动手做的收获很大。

Exercise 4.1.1. Verify that the definition of equality on the integers is both reflexive and symmetric.
Solution:
Reflexive: $a+b=a+b \implies a\text{---} b=a\text{---} b$
Symmetric: $a\text{---} b=c\text{---} d \implies a+d=c+b \implies c+b=a+d \implies c\text{---} d=a\text{---} b$

$\blacksquare$

Exercise 4.1.2. Show that the definition of negation on the integers is well-defined in the sense that if $(a\text{---}b)=(a'\text{---}b')$ , then $-(a\text{---}b)=-(a'\text{---}b')$ (so equal integers have equal negations).
Solution: We have

$\begin{aligned} a\text{---} b=a'\text{---} b' &\implies a+b'=a'+b\\&\implies b+a'=b'+a \\&\implies b\text{---} a=b' \text{---} a'\\&\implies -(a\text{---} b)=-(a'\text{---} b') \end{aligned}$

$\blacksquare$

Exercise 4.1.3. Show that $(-1)\times a=-a$ for every integer $a$ .
Solution: If $a$ is positive

$\begin{aligned}(-1)\times a&=(0\text{---} 1)\times (a\text{---} 0)\\&=(0\cdot a+1\cdot 0)-(1\cdot a+0\cdot 0)=0\text{---} a=-a\end{aligned}$

If a is zero, then $(-1)\times 0=0$ , and

$-a=0\text{---} a=0\text{---} 0=0$

If $a$ is negative, then there’s a positive natural number $b$ such that $a=-b$ , so

$\begin{aligned}(-1)\times a&=(0\text{---} 1)\times (0\text{---} b)\\&=(0\cdot 0+1\cdot b)-(0\cdot b+1\cdot 0)=b=-a\end{aligned}$

$\blacksquare$

Exercise 4.1.4. Prove the remaining identities in Proposition 4.1.6.
Solution:
(1) $x+y=y+x$
Write $x=a\text{---} b,y=c\text{---} d$ , then use commutative addition in $\mathbf N$ :

$\begin{aligned}x+y&=(a\text{---} b)+(c\text{---} d)=(a+c)\text{---} (b+d)\\&=(c+a)\text{---} (d+b)=(c\text{---} d)+(a\text{---} b)=y+x\end{aligned}$

(2) $(x+y)+z=x+(y+z)$
Write $x=a\text{---} b,y=c\text{---} d,z=e\text{---} f$ , then

$(x+y)+z=(a+c)\text{---} (b+d)+(e\text{---} f)=(a+c+e)\text{---} (b+d+f)\\x+(y+z)=(a\text{---} b)+[(c+e)\text{---} (d+f)]=(a+c+e)\text{---} (b+d+f)$

(3) $x+0=0+x=x$
Let $y=0$ in (1) we get $x+0=0+x$ , and $x+0=(a\text{---} b)+(0\text{---} 0)=(a\text{---} b)=x$

(4) $x+(-x)=(-x)+x=0$
Let $y=-x$ in (1) we get $x+(-x)=(-x)+x$ , and
$x+(-x)=(a\text{---} b)+(b\text{---} a)=(a+b)\text{---} (b+a)$
As $a+b+0=a+b+0,(a+b)\text{---} (b+a)=0\text{---} 0=0$

(5) $xy=yx$
Write $x=a\text{---} b,y=c\text{---} d$ , then use commutative addition in $\mathbf N$ :

$xy=(ac+bd)\text{---} (ad+bc)=(ca+db)\text{---} (bc+ad)=yx$

(6) $(xy)z=x(yz)$
Already proved in the text.

(7) $x1=1x=x$
By (5) $x1=1x$ , and

$x1=(a\text{---} b)(1\text{---} 0)=(a\cdot 1+b\cdot 0)\text{---} (a\cdot 0+b\cdot 1)=a\text{---} b=x$

(8) $x(y+z)=xy+xz$
We can verify

$\begin{aligned}x(y+z)&=(ab)\times ((c+e)\text{---} (d+f))\\&=ac+bd+ae+bf)\text{---} (ad+bc+af+be)\end{aligned}\\ \begin{aligned}xy+xz&=((ac+bd)\text{---} (ad+bc))+((ae+bf)\text{---}(af+be))\\&=(ac+bd+ae+bf)\text{---} (ad+bc+af+be)\end{aligned}$

(9) $(y+z)x=yx+zx$
By (8) and (5) the result is proved.

$\blacksquare$

Exercise 4.1.5. Prove Proposition 4.1.8.
Solution: Since $-a=0\text{---} a$ , we have $a=0 \iff -a=0$ . So let $a,b\in \mathbf Z,ab=0$ , then:
If $a,b\in \mathbf N,ab=0\implies (a=0)\vee (b=0)$ by Lemma 2.3.3
If $a\notin \mathbf N$ , then $-a=(-1)\times a\in \mathbf N$ by Exercise 4.1.3, so

$ab=0\implies -(ab)=0\implies (-1)\times ab=0\implies (-a)b=0$

Thus if $b\in \mathbf N$ , by Lemma 2.3.3 we have $(-a=0)\vee (b=0)$ , which means $b=0$ .
if $b\notin N$ , then

$\begin{aligned}(-a)b=0&\implies b(-a)=0\implies -[b(-a)]=0\\&\implies (-b)(-a)=0\implies (-a=0)\vee (-b=0)\\&\implies (a=0)\vee (b=0)\end{aligned}$

This is a contradiction.

$\blacksquare$

Exercise 4.1.6. Prove Corollary 4.1.9.
Solution: Since $c\neq 0$ , use Proposition 4.1.8 we can get:

$\begin{aligned}ac=bc &\implies ac-bc=bc-bc=0 \\&\implies (a-b)c=0 \implies (a-b)=0\\&\implies (a-b)+b=0+b \implies a=b\end{aligned}$

$\blacksquare$

Exercise 4.1.7. Prove Lemma 4.1.11.
Solution:
( a ) We have

$\begin{aligned}a>b &\iff (a\geq b)\wedge (a\neq b)\\&\iff (a=b+c,c\in N)\wedge (a\neq b)\\&\iff (a-b=c)\wedge (a-b\neq 0)\\&\iff a-b \text{ is a positive natural number }\end{aligned}$

( b ) We have

$\begin{aligned}a>b &\implies (a-b=d,d\text{ is positive})\\&\implies (a+c+(-c)-b=d) \\&\implies (a+c)+(-1)(c+b)=d \\&\implies (a+c)-(b+c)=d \\&\implies a+c>b+c\end{aligned}$

( c ) $a>b \implies (a-b=d,d\text{ is positive})\implies ac-bc=dc$
Since both $d$ and $c$ are positive, by Lemma 2.3.3 $dc$ is positive, thus $ac>bc$

( d ) We have

$\begin{aligned}a>b &\implies (a-b=d,d\text{ is positive})\\&\implies -b+a=d\\&\implies -b-(-a)=d\\&\implies -b>-a\end{aligned}$

( e ) We have

$\begin{aligned}(a>b)\wedge (b>c)&\implies (a-b=d,d\text{ is positive})\wedge (b-c=e,e\text{ is positive})\\&\implies (a-b)+(b-c)=a-c=d+e \\&\implies a>c\end{aligned}$

( f ) $a-b=a+(-b)\in \mathbf Z$ , so by Lemma 4.1.5, exactly one of the three statements is true:

$a-b>0,\quad a-b=0,\quad a-b<0$

which is the result.

$\blacksquare$

Exercise 4.1.8. Show that the principle of induction (Axiom 2.5) does not apply directly to the integers. More precisely, give an example of a property $P(n)$ pertaining to an integer $n$ such that $P(0)$ is true, and that $P(n)$ implies $P(n++)$ for all integers $n$ , but that $P(n)$ is not true for all integers $n$ . Thus induction is not as useful a tool for dealing with the integers as it is with the natural numbers.
Solution: Let $P(n)=\{n\in \mathbf Z:n\geq -1\}$ , then $P(0)$ is true, and if $P(n)$ is true, it’s obvious that $P(n++)$ is true. However $P(-2)$ is false.

$\blacksquare$

陶哲轩实分析3.6及习题-Analysis I 3.6

2019年4月4日2021年8月14日christangdt18条评论

这一节戏称如何数数，由于仅限制在有限集合上，所以并不难理解，但是最开始采用了规范的集合元素个数相等的定义（有一个bijection存在），便于以后拓展到无限维的情况。集合cardinality相等是一种等价关系（满足自反、对称、传递），并且是唯一的。有限集合cardinality的运算其实可以等价到自然数运算上。

Exercise 3.6.1. Prove Proposition 3.6.4.

Solution: $X$ has equal cardinality with $X$ : we have the bijection $f:X\to X$ as $f(x)=x,\forall x\in X$
If $X$ has equal cardinality with $Y$ : then there’s a bijection $f$ from $X$ to $Y$ , thus the function $f^{-1}$ is a bijection from $Y$ to $X$ .
If $X$ has equal cardinality with $Y$ , and $Y$ has equal cardinality with $Z$ , then we can find bijection $f:X\to Y$ and $g:Y\to Z$ , due to Exercise 3.3.7, $g\circ f:X\to Z$ is bijective.

$\blacksquare$

Exercise 3.6.2. Show that a set $X$ has cardinality 0 if and only if $X$ is the empty set.

Solution: If $X=\emptyset$ , then the empty function $f:\emptyset \to \{i\in \mathbf N:1\leq i\leq 0\}$ is a bijection.
If $X$ has cardinality $0$ , and suppose $x\in X$ , then define $f(x)=1$ , we can see $\{x\}$ has cardinality $1$ , thus $X$ has cardinality at least $1$ , a contradiction.

$\blacksquare$

Exercise 3.6.3. Let $n$ be a natural number, and let $f:\{i\in \mathbf N\}\to \mathbf N$ be a function. Show that there exists a natural number $M$ such that $f(i)\leq M$ for all $1\leq i\leq n$ .

Solution: We induct on $n$ : when $n=0$ the statement is meaningless. When $n=1, f(1)\in \mathbf N$ , we can choose $M=f(1)++$ and the statement is true.
Now suppose for $n$ , we can choose $M$ such that for function $f$ , we have $f(i)\leq M,1\leq i\leq n$ , then for $n+1$ , let $f:\{i\in \mathbf N:1\leq i\leq n+1\}\to N$ be a function, then $f$ restricted on $\{i\in \mathbf N:1\leq i\leq n\}$ is a function satisfy the induction hypothesis, and there’s a $M$ such that $f(i)\leq M,1\leq i\leq n$ . Now if $f(n+1)>M$ , we refresh $M$ to be $f(n+1)$ , then the new $M$ has the property $f(i)\leq M,1\leq i\leq n+1$ . So the statement is true.

$\blacksquare$

Exercise 3.6.4. Prove Proposition 3.6.14.

Solution:
( a ) let $\#(X)=n$ , then we can find a bijection $f:X\to\{1,\dots,n\}$ , .define $g$ which equals $f$ on $\{1,\dots,n\}$ and $g(x)=n+1$ , then $g$ is a bijection from $\#(X\cup \{x\})$ to $\{1,\dots,n+1\}$ .

( b ) we know that $\#(X)$ and $\#(Y)$ are finite. Let $\#(X)=n,\#(Y)=m$ , and let the bijection from $X$ to $\{i\in \mathbf N:1\leq i\leq n\}$ to be $f$ , the bijection from $Y$ to $\{i\in \mathbf N:1\leq i\leq m\}$ to be $g$ . Now define a function $h$ as follows:

$h(x)=f(x),\quad x\in X \\ h(y)=g(y)+n,\quad y\in Y,y\notin X$

if no $y\in X$ , then $X\cap Y=\emptyset$ , and $h:X\cup Y\to \{i\in N:1\leq i\leq m+n\}$ is a bijection. Thus

$\#(X\cup Y)=\#(X)+\#(Y)$

If there’s a $y\in X$ , then $h$ maps $X\cup Y$ to a subset of $\{i\in \mathbf N:1\leq i\leq n+m\}$ , which can be bijectively mapped to $\{i\in \mathbf N:1\leq i\leq k\},k<m+n$ , thus

$\#(X\cup Y)\leq \#(X)+\#(Y)$ .

( c ) $Y\subseteq X$ means $Y\cup (X\backslash Y)=X$ and $Y\cap X\backslash Y=\emptyset$ , thus

$\#(X)=\#(Y\cup (X\backslash Y))=\#(Y)+\#(X\backslash Y)$

So $\#(Y)\leq \#(X)$ . If $Y\neq X$ , then $X\backslash Y\neq \emptyset$ , so $\#(X\backslash Y)\geq 1$ , thus $\#(Y)<\#(X)$ .

( d ) If $f$ is one-to-one, then $f:X\to f(X)$ is a bijection, thus $\#(f(X))=\#(X)$ . In general cases, $f(X)$ is a subset of a hypothetical one-to-one function image, which has equal cardinality with $X$ , thus use ( c ) one can get $\#(f(X))\leq \#(X)$ .

( e ) Let $\#(X)=m$ and we use induction on $\#(Y)=n\in \mathbf N$ .
If $n=0$ then $Y=\emptyset$ by Exercise 3.6.2, then $X\times Y=\emptyset \implies \#(X\times Y)=0=\#(X)\times \#(Y)$ . If $n=1$ then $Y=\{y\}$ is a singleton set, and then $X\times Y=X\times \{y\}$ , we can construct a bijection $f:X\to X\times \{y\}$ by setting $f(x)=(x,y),x\in X$ , thus $\#(X)=\#(X\times \{y\})=m$ .
Now suppose the conclusion holds for all $Y,\#(Y)\leq n$ , and $Y'$ is a set, $\#(Y')=n++$ . Then $Y'$ is nonempty, and $\exists y\in Y'$ , now $\#(Y'-\{y\})=(n++)-1=n$ , moreover

$X\times Y'=\big(X\times (Y'-\{y\})\big)\cup (X\times \{y\})\\ \big(X\times (Y'-\{y\})\big)\cap (X\times \{y\})=\emptyset$

So $X\times Y'$ is finite by ( b ) and $\#(X\times Y')=\#\big(X\times (Y'-\{y\})\big)+\#(X\times \{y\})$ . Now by induction hypothesis

$\#\big(X\times (Y'-\{y\})\big)=\#(X)\times \#(Y'-\{y\})=mn \\ \#(X\times \{y\})=\#(X)\times \#(\{y\})=m$

We have $\#(X\times Y')=mn+m=m(n++)$ , and the conclusion is true.

( f ) Let $\#(Y)=m$ and we use induction on $\#(X)=n\in N$
If $n=0$ then $X=\emptyset$ by Exercise 3.6.2, then there’s only the empty function from $X$ to $Y$ . Thus $\#(Y^X )=1=m^0$ .
Now suppose $\#(X)=k\in N\implies \#(Y^X )=m^k$ , consider any set $X',\#(X')=k++$ , as $X'$ is nonempty, and $\exists x\in X'$ , let $X=X'-\{x\}$ , then there’s a bijection $h:Y^{X'}\to Y^X\times Y^{\{x\}}$ defined by

$h(f(X'))=\big(f(X),f(\{x\})\big)$

thus $\#(Y^{X'})=\#(Y^X\times Y^{\{x\}})=\#\left(Y^X \right)\times \#\left(Y^{\{x\}}\right)=m^k\times m=m^{k++}$ , and the induction conclusion is true.

$\blacksquare$

Exercise 3.6.5. Let $A$ and $B$ be sets. Show that $A\times B$ and $B\times A$ have equal cardinality by constructing an explicit bijection between the two sets. Then use Proposition 3.6.14 to conclude an alternate proof of Lemma 2.3.2.

Solution: We have a bijection $f:A\times B\to B\times A$ defined by
$f(a,b)=(b,a),\quad \forall (a,b)\in A\times B$
An alternate proof of Lemma 2.3.2:
Let $A,B$ be finite sets with cardinality $m$ and $n$ , then $\#(A\times B)=m\times n$ and $\#(B\times A)=n\times m$ , since there’s a bijection between the two sets, $\#(A\times B)=\#(B\times A)$ .

$\blacksquare$

Exercise 3.6.6. Let $A,B,C$ be sets. Show that the set $(A^B)^C$ and $A^{B\times C}$ have equal cardinality by constructing an explicit bijection between the two sets. Conclude that $(a^b)^c=a^{bc}$ for any natural numbers $a,b,c$ . Use a similar argument to also conclude $a^b\times a^c=a^{b+c}$ .

Solution: $(A^B )^C$ means the set of all functions from $C$ to $A^B$ , $A^{B\times C}$ means the set of all functions from $B\times C$ to $A$ . If $F\in (A^B )^C,F:C\to A^B$ , then $\forall c\in C,F(c):B\to A$ . We define a map $h$ from $(A^B )^C$ to $A^{B\times C}$ as follows:

$h(F)=G\in A^{B\times C} \text{ s.t. } G(b,c)=[F(c)]b,\quad \forall b\in B,c\in C$

then $h$ is a bijection, thus $\# \left((A^B )^C \right)=\#(A^{B\times C} )$ . Use Proposition 3.6.14 ( e )( f ) several times we can get $(a^b )^c=a^{bc}$ if $\#(A)=a,\#(B)=b,\#(C)=c$ .
To prove $a^b\times a^c=a^{b+c}$ , we just need to show a bijection from $A^B\times A^C$ to $A^{B\cup C}$ if $B\cap C=\emptyset$ . For $\forall (f,g)\in A^B\times A^C$ ,i.e. $f:B\to A,g:C\to A$ , let $H(f,g)(x)=f(x),x\in B$ and $H(f,g)(x)=g(x),x\in C$ , then it’s easy to see that $H:A^B\times A^C\to A^{B\cup C}$ is bijective.

$\blacksquare$

Exercise 3.6.7. Let $A$ and $B$ be sets. Let us say that $A$ has lesser or equal cardinality to $B$ if there exists an injection $f:A\to B$ from $A$ to $B$ . Show that if $A$ and $B$ are finite sets, then $A$ has lesser or equal cardinality to $B$ if and only if $\# (A)\leq \# (B)$ .

Solution: If $A$ has lesser or equal cardinality to $B$ , then there’s an injection $f:A\to B$ , thus $f:A\to f(A)$ is a bijection, so $\#(A)=\#(f(A))\leq \#(B)$ since $f(A)\subseteq B$ .
If $\#(A)\leq \#(B)$ , then let $\#(A)=m,\#(B)=n$ , so $m\leq n$ and we can find bijections

$f:A\to \{i\in \mathbf N:1\leq i\leq m\},\quad g:B\to \{i\in \mathbf N:1\leq i\leq n\}$

Thus the function $h=g^{-1}\circ f$ maps $A$ to $B$ .
To show $h$ is injective, we suppose $h(x)=h(y)$ , then $g^{-1}\left(f(x)\right)=g^{-1} (f(y))$ by definition, and use $g$ at both sides we can get $f(x)=f(y)$ , by $f$ is a bijection we can get $x=y$ .

$\blacksquare$

Exercise 3.6.8. Let $A$ and $B$ be sets such that there exists an injection $f:A\to B$ from $A$ to $B$ .(i.e., $A$ has lesser or equal cardinality to $B$ ). Show that there exists a surjection $g:B\to A$ from $B$ to $A$ . (The converse to this statement requires the axiom of choice; see Exercise 8.4.3.)

Solution: If $A=\emptyset$ then as $g:B\to \emptyset$ is surjective for any set $B$ , the statement is true.
Now suppose $A\neq \emptyset$ , then $\exists a\in A$ , define $g:B\to A$ as follows:

$g(x)=f^{-1} (x),x\in f(A),\quad g(x)=a,x\in B\backslash f(A)$

$g$ is successfully defined since $f$ is injective.
To show that $g$ is surjective, choose $\forall y\in A$ , then $f(y)\in B$ , and $g(f(y))=f^{-1}(f(y))=y$ , so $f(y)$ is the element whose image under $g$ is $y$ .

$\blacksquare$

Exercise 3.6.9. Let $A$ and $B$ be finite sets. Show that $A\cup B$ and $A\cap B$ are also finite sets, and that $\#(A)+\#(B)=\#(A\cup B)+\#(A\cap B)$ .

Solution: $A\cup B$ is finite by Proposition 3.6.14(b)
$A\cap B$ is finite by $A\cap B\subseteq A$ and Proposition 3.6.14( c )
Since $A=(A\backslash B)\cup (A\cap B),(A\backslash B)\cap (A\cap B)=\emptyset$ , we have $\#(A)=\#(A\backslash B)+\#(A\cap B)$
By the same logic, $\#(B)=\#(B\backslash A)+\#(A\cap B)$
Since $A\cup B=(A\backslash B)\cup (B\backslash A)\cup (A\cap B)$ , all three sets are disjoint with each other,

$\#(A\cup B)=\#(A\backslash B)+\#(B\backslash A)+\#(A\cap B)$

Joining the three equations and the conclusion follows.

$\blacksquare$

Exercise 3.6.10. Let $A_1,\dots,A_n$ be finite sets such that $\#(\bigcup_{i\in \{1,\dots,n\}}A_i)>n$ . Show that there exists $i\in \{1\dots,n\}$ such that $\#(A_i)\geq 2$ . (This is known as the pigeonhole principle.)

Solution: Assume there’s no $i\in \{1,\dots ,n\}$ such that $\#(A_i )\geq 2$ , then we have

$\#(A_i )\leq 1,\quad \forall i\in \{1,\dots ,n\}$

Use Proposition 3.6.14(b) $n$ times we can get

$\#\left(\bigcup_{i\in \{1,\dots ,n\}}A_i \right)\leq \#(A_1 )+\dots+\#(A_n )\leq n$

Which leads to a contradiction.

$\blacksquare$

陶哲轩实分析3.5及习题-Analysis I 3.5

2019年4月4日2020年9月25日christangdt31条评论

这一节说的是Cartesian Products，中文翻译成笛卡尔乘积，实质是用向量的形式将一维的集合扩展为二维至多维，通过有序对ordered pair定义Cartesian Products，单纯的集合其实可以看做Cartesian Products 在一维上的限制，最后还说了finite choice，即从每个n-tuple里拿出一个分量是可行的，但是无限维的情况却需要axiom of choice，后者直到第八章才会提及。

Exercises 3.5.1. Suppose we define the ordered pair $(x,y)$ for any objects $x$ and $y$ by the formula $(x,y):=\{\{x\},\{x,y\}\}$ (thus using several applications of Axiom 3.3). Thus for instance $(1,2)$ is the set $\{\{1\},\{1,2\}\}$ , $(2,1)$ is the set $\{\{2\},\{2,1\}\}$ , and $(1,1)$ is the set $\{\{1\}\}$ . 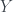Show that such a definition indeed obeys the propert (3.5), and also whenever $X$ and $Y$ are sets, the Cartesian product $X\times Y$ is also a set. Thus this definition can be validly used as a definition of an ordered pari. For an additional challenge, show that the alternate definition $(x,y):=\{x,\{x,y\}\}$ also verifies (3.5) ans is thus also an acceptable definition of ordered pair.

Solution:
Verify such a definition obeys the property (3.5):

$\begin{aligned}(x,y)=(x',y')&\iff \{\{x\},\{x,y\}\}=\{\{x'\},\{x',y'\}\}\\&\iff (\{x\}=\{x'\})\wedge (\{x,y\}=\{x',y'\})\\&\iff (x=x')\wedge (y=y')\end{aligned}$

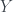If $X$ and $Y$ are sets, use axiom of replacement, we have, given any object $y$ , $A=\{(x,y):x\in X\}$ is a set, we name it $A_y$ . Then, use axiom of replacement again, $A=\{A_y:y\in Y\}$ is a set. Finally we have $X\times Y=\bigcup A$ .
Additional challenge:
Verify definition $(x,y):=\{x,\{x,y\}\}$ obeys the property (3.5):

$(x,y)=(x',y')\iff \{x,\{x,y\}\}=\{x',\{x',y'\}\}$

Now if $x\in \{x',\{x',y'\}\}$ , then either $x=x'$ or $x=\{x',y'\}$ . Suppose $x=\{x',y'\}$ , then $x$ is a set, furthermore we shall get $x'=\{x,y\}$ , which is also a set, then we have $(x\in x')\wedge (x'\in x)$ , a contradiction to Exercise 3.2.2.
So the only possible outcome is $x=x'$ , thus $\{x,y\}=\{x',y'\}$ and $y=y'$ .
The other direction is easy to prove.

$\blacksquare$

Exercises 3.5.2. Suppose we define an ordered $n$ -tuple to be a surjective function $x:{i\in \mathbf N:1\leq i\leq n}\to X$ whose range is some arbitrary set $X$ (so different ordered $n$ -tuples are allowed to have different ranges); we then write $x_i$ for $x(i)$ , and also write $x$ as $(x_i)_{1\leq i\leq n}$ . Using this definition, verify that we have $(x_i)_{1\leq i\leq n}=(y_i)_{1\leq i\leq n}$ if and only if $x_i=y_i$ for all $1\leq i\leq n$ . Also, show that if $(X_i)_{1\leq i\leq n}$ are an ordered $n$ -tuple of sets, then the Cartesian product, as defined in Definition 3.5.7, is indeed a set.

Solution: First we have

$(x_i)_{1\leq i\leq n}=(y_i)_{1\leq i\leq n} \iff x(i)=y(i),1\leq i\leq n\iff x_i=y_i,1\leq i\leq n$

Next, every ordered $n$ -tuple is a function $f:\{i\in \mathbf N:1\leq i\leq n\}\to X$ , if we define

$X=\bigcup_{1\leq i\leq n}X_i$

Then the set $X$ contains every element of $X_1$ to $X_n$ . Thus using Exercise 3.4.7, the collection of all partial functions whose domain is $\{i\in N:1\leq i\leq n\}$ and range $X$ forms a set. Now use the axiom of specification there’s a set

$\{f:f(i)\in X_i, 1\leq i\leq n\}$

which satisfies definition 3.5.7.

$\blacksquare$

Exercises 3.5.3. Show that the definitions of equality for ordered pari and ordered $n$ -tuple obey the reflexivity, symmetry and transitivity axioms.

Solution: We directly prove ordered n-typle:
Reflexivity:
$(x_i=x_i,1\leq i\leq n)\implies (x_i)_{1\leq i\leq n}=(x_i)_{1\leq i\leq n}$
Symmetry:
$\begin{aligned}(x_i)_{1\leq i\leq n}=(y_i)_{1\leq i\leq n}&\implies x_i=y_i,1\leq i\leq n\\&\implies y_i=x_i,1\leq i\leq n\\&\implies (y_i)_{1\leq i\leq n}=(x_i)_{1\leq i\leq n}\end{aligned}$
Transitivity:
from $(x_i)_{1\leq i\leq n}=(y_i)_{1\leq i\leq n}\implies x_i=y_i,1\leq i\leq n$ and $(y_i)_{1\leq i\leq n}=(z_i)_{1\leq i\leq n}\implies y_i=z_i,1\leq i\leq n$ , we have $x_i=z_i,1\leq i\leq n\implies (x_i)_{1\leq i\leq n}=(z_i)_{1\leq i\leq n}$ .

$\blacksquare$

Exercises 3.5.4. Let $A,B,C$ be sets. Show that $A\times (B\cup C)=(A\times B)\cup (A\times C)$ , that $A\times (B\cap C)=(A\times B)\cap (A\times C)$ , and that $A\times (B\backslash C)=(A\times B)\backslash (A\times C)$ . (one can of course prove similar identities in which the roles of the left and right factors of the Cartesian product are reversed.)

Solution: We have

$\begin{aligned}(x,y)\in A\times (B\cup C)&\iff (x\in A)\wedge (y\in B\cup C)\\&\iff (x\in A)\wedge \big((y\in B)\vee (y\in C)\big)\\&\iff \big((x\in A)\wedge (y\in B)\big)\vee \big((x\in A)\wedge (y\in C)\big)\\&\iff \big((x,y)\in (A\times B)\big)\vee \big((x,y)\in (A\times C)\big)\end{aligned}$

So that $A\times (B\cup C)=(A\times B)\cup (A\times C)$
Next,

$\begin{aligned}(x,y)\in A\times (B\cap C)&\iff (x\in A)\wedge (y\in B\cap C)\\&\iff (x\in A)\wedge (y\in B)\wedge (y\in C)\\&\iff \big((x\in A)\wedge (y\in B)\big)\wedge \big((x\in A)\wedge (y\in C)\big)\\&\iff \big((x,y)\in (A\times B)\big)\wedge \big( (x,y)\in (A\times C) \big)\end{aligned}$

So that $A\times (B\cap C)=(A\times B)\cap (A\times C)$
Finally,

$\begin{aligned}(x,y)\in A\times (B\backslash C)&\iff (x\in A)\wedge (y\in B\backslash C)\\&\iff (x\in A)\wedge (y\in B)\wedge (y\notin C)\\&\iff \big((x\in A)\wedge (y\in B)\big)\wedge \big((x\in A)\wedge (y\notin C)\big)\\&\iff \big((x,y)\in (A\times B)\big)\wedge \big((x,y)\notin (A\times C)\big)\end{aligned}$

So that $A\times (B\backslash C)=(A\times B)\backslash (A\times C)$ .

$\blacksquare$

Exercises 3.5.5. Let $A,B,C,D$ be sets. Show that $(A\times B)\cap(C\times D)=(A\cap C)\times (B\cap D)$ . Is it true that $(A\times B)\cup(C\times D)=(A\cup C)\times (B\cup D)$ ? Is it true that $(A\times B)\backslash (C\times D)=(A\backslash C)\times (B\backslash D)$ ?

Solution: First we have

$\begin{aligned}(x,y)\in (A\times B)\cap (C\times D)&\iff \big((x,y)\in A\times B\big)\wedge \big((x,y)\in C\times D\big)\\&\iff (x\in A)\wedge (y\in B)\wedge (x\in C)\wedge (y\in D)\\&\iff (x\in A\cap C)\wedge (y\in B\cap D)\\&\iff (x,y)\in (A\cap C)\times (B\cap D)\end{aligned}$

Next, the two statement are both false.
If $A=\{1\},B=\{2\},C=\{3\},D=\{4\}$ , then

$(A\times B)\cup (C\times D)=\{(1,2),(3,4)\},\\(A\cup C)\times (B\cup D)=\{(1,2),(1,4),(3,2),(3,4)\}$

If $A=\{1,2\},B=\{3,4\},C=\{1\},D=\{3\}$ , then

$(A\times B)\backslash (C\times D)=\{(1,4),(2,3),(2,4)\},\\(A\backslash C)\times (B\backslash D)=\{(2,4)\}$

$\blacksquare$

Exercises 3.5.6. Let $A,B,C,D$ be non-empty sets. Show that $A\times B\subseteq C\times D$ if and only if $A\subseteq C$ and $B\subseteq D$ , and that $A\times B= C\times D$ if and only if $A=C$ and $B=D$ . What happens if the hypotheses that the $A,B,C,D$ are all non-empty are removed?

Solution: First, we have

$\begin{aligned}(A\times B\subseteq C\times D)&\iff \forall (x,y)\in A\times B,(x,y)\in C\times D\\&\iff \big((\forall x\in A,\forall y\in B)\implies x\in C,y\in D\big)\\&\iff (\forall x\in A\implies x\in C)\wedge (\forall y\in B\implies y\in D)\\&\iff (A\subseteq C)\wedge (B\subseteq D)\end{aligned}$

Next, use this result we have

$\begin{aligned}(A\times B=C\times D)&\iff (A\times B\subseteq C\times D)\wedge (C\times D\subseteq A\times B)\\&\iff (A\subseteq C)\wedge (B\subseteq D)\wedge (C\subseteq A)\wedge (D\subseteq B)\\&\iff (A=C)\wedge (B=D)\end{aligned}$

If non-empty hypothesis are removed, then both statements may be wrong.

$\blacksquare$

Exercises 3.5.7. Let $X,Y$ be sets, and let $\pi_{X\times Y\to X}:X\times Y\to X$ and $\pi_{X\times Y\to Y}:X\times Y\to Y$ be the maps $\pi_{X\times Y\to X}(x,y):=x$ and $\pi_{X\times Y\to Y}(x,y):=y$ ; these maps are known as the co-ordinate functions on $X\times Y$ . Show that for any functions $f:Z\to X$ and $g:Z\to Y$ , there exists a unique function $h:Z\to X\times Y$ such that $\pi_{X\times Y\to X}\circ h=f$ and $\pi_{X\times Y\to Y}\circ h=g$ . 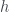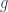(Compare this to the last part of Exercise 3.3.8, and to Exercise 3.1.7.) This function $h$ is known as the direct sum of $f$ and $g$ and is denoted $h=f\oplus g$ .

Solution:
We define $h(z)=\left(f(z),g(z)\right),\forall z\in Z$ . Then

$(\pi_{X\times Y\to X}\circ h)(z)=\pi_{X\times Y\to X}(h(z))=\pi_{X\times Y\to X}(f(z),g(z))=f(z)\\(\pi_{X\times Y\to Y}\circ h)(z)=\pi_{X\times Y\to Y}(h(z))=\pi_{X\times Y\to Y}(f(z),g(z))=g(z)$

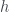To prove $h$ is unique, suppose there’s $h':Z\to X\times Y$ satisfy the condition, then $\forall z\in Z$ , let $h'(z)=(a,b)$ , and we have

$(\pi_{X\times Y\to X}\circ h')(z)=f(z)=a,\quad (\pi_{X\times Y\to Y}\circ h)(z)=g(z)=b$

This means $h'(z)=h(z)$ , thus $h=h'$ .

$\blacksquare$

Exercises 3.5.8. Let $X_1,\dots,X_n$ be sets. Show that the Cartesian product $\prod_{i=1}^nX_1$ is empty if and only if at least one of the $X_i$ is empty.

Solution: If one of the $X_i$ is empty, then obviously $\prod_{i=1}^nX_i$ is empty.
On the other hand, if $\prod_{i=1}^nX_i$ is empty and no $X_i$ is empty, then by Lemma 3.5.12, $\prod_{i=1}^nX_i$ must be non-empty and leads to a contradiction.

$\blacksquare$

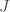Exercises 3.5.9. Suppose that $I$ and $J$ are two sets, and for all $\alpha \in I$ let $A_{\alpha}$ be a set, and for all $\beta \in J$ let $B_{\beta}$ be a set. Show that $(\bigcup_{\alpha\in I}A_{\alpha})\cap(\bigcup_{\beta \in J}B_{\beta})=\bigcup_{(\alpha, \beta)\in I\times J}(A_{\alpha}\cap B_{\beta})$ .

Solution: We have

$\begin{aligned}x\in (\cup_{\alpha \in I}A_{\alpha})\cap (\cup_{\beta \in J}B_{\beta})&\iff (x\in \cup_{\alpha \in I}A_{\alpha})\wedge (x\in \cup_{\beta \in J}B_{\beta})\\&\iff (\exists a\in I,x\in A_a)\wedge (\exists b\in J,x\in B_b)\\&\iff \exists (a,b)\in I\times J,(x\in A_a )\wedge (x\in B_b)\\&\iff \exists (a,b)\in I\times J,x\in (A_a\cap B_b)\\&\iff x\in \cup_{(\alpha,\beta)\in I\times J}(A_a\cap B_b)\end{aligned}$

$\blacksquare$

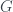Exercises 3.5.10. If $f:X\to Y$ is a function, define the graph of $f$ to be the subset of $X\times Y$ defined by ${(x,f(x)):x\in X}$ . Show that two functions $f:X\to Y,\widetilde{f}:X\to Y$ are equal if and only if they have the same graph. 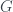Conversely, if $G$ is any subset of $X\times Y$ with the property that for each $x\in X$ , the set ${y\in Y:(x,y)\in G}$ has exactly one element ( or in other words, $G$ obeys the vertical line test), show that there is exactly one function $f:X\to Y$ whose graph is equal to $G$ .

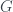Solution: On one hand we have

$f=\widetilde{f}\iff \forall x\in X,f(x)=\widetilde{f}(x)\iff \forall x\in X,(x,f(x))=(x,\widetilde{f}(x))$

Conversely, define the function $f:X\to Y$ as follows: $f(x)=y$ such that $(x,y)\in G$ , by the given condition $f$ can be defined successfully, by the previous result there’s only one $f$ since every function satisfy the condition has the same graph.

$\blacksquare$

Exercises 3.5.11. Show that Axiom 3.10 can in fact be deduced from Lemma 3.4.9 and the other axioms of set theory, and thus Lemma 3.4.9 can be used as an alternate formulation of the power set axiom.

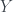Solution: For any two sets $X$ and $Y$ , the collection

$X\times Y=\{(x,y),x\in X,y\in Y\}$

is a set. Thus by lemma 3.4.9, all subsets of $X\times Y$ is a set. Use the axiom of specification, the collection

$V=\{G\subset 2^{X\times Y}:G \text{ obeys the vertical line test}\}$

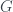is a set. By Exercise 3.5.10, for every $G\in V$ , there’s exactly one function $f:X\to Y$ whose graph is equal to $G$ . Use the axiom of replacement, there’s a set

$\{f:f \text{ has the graph }G,G\in X\times Y\}$

This set is equal to $Y^X$ .

$\blacksquare$

Exercises 3.5.12. This exercise will establish a rigorous version of Proposition 2.1.16. Let $f:\mathbf N \times \mathbf N\to \mathbf N$ be a function, and let $c$ be a natural number. Show that there exists a function $a:\mathbf N \to \mathbf N$ such that

$a(0)=c$

and

$a(n++)=f(n,a(n)) \text{ for all }n\in \mathbf N$ ,

and furthermore that this funtion is unique.
For an additional challenge, prove this resul without using any properties of the natural numbers other that the Peano axioms directly (in particular, without using the ordering of the natural numbers, and without appealing to Proposition 2.1.16).

Solution:
First we prove for $\forall N\in \mathbf N$ , there exists a function

$a_N:\{n\in \mathbf N:n\leq N\}\to \mathbf N$

such that $a_N(0)=c,a_N(n++)=f(n,a_N(n))$ for $n\in \mathbf N,n<N$ . Use induction.
For $N=0$ , let $a_0 (0)=c$ .
Suppose $N=k$ , the conclusion is true, then for $N=k+1$ , let $a_{k+1}:\{n\in \mathbf N:n\leq k+1\}\to \mathbf N$ defined as follows:

$a_{k+1} (i)=a_k (i),i\leq k,\quad a_{k+1} (k+1)=f(k,a_k (k))$

It’s easy to see that $a_{k+1}$ satisfy the condition.
Now we prove the existence of $a$ . In fact the function $a:\mathbf N \to \mathbf N$ defined by $a(0)=0, a(N)=a_N(N)$ is the function we want.
If there’s another function 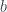$b$ satisfy the result, then it’s easy to use induction to prove that $a(n)=b(n),\forall n\in \mathbf N$

Additional challenge:
First I prove for every $N\in \mathbf N$ , there exists one and only one pair of subsets $A_N,B_N$ , such that:
( a ) $A_N\cap B_N=\emptyset$
( b ) $A_N\cup B_N=N$
( c ) $0\in A_N$
( d ) $N++\in B_N$
( e ) $n\in B_N\implies n++\in B_N$
( f ) $(n\in A_N )\wedge (n\neq N)\implies n++\in A_N$
Step 1: for $0\in N$ , we have $A_0=\{0\},B_0=\{1,2,\dots\}$ , and it’s easy to see the pair is unique, since if there’s another pair $A_0',B_0'$ satisfy condition (a)-(f), then by (c) we have $0\in A_0'$ , so there should be another integer $k\neq 0,k\in A_0'$ , but $0++\in B_0'$ by (d), and by (e) we can deduce $k\in B_0'$ eventually, which is a contradiction to (a)
Step 2: suppose for 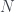$N$ , we have found a unique pair of sets $A_N,B_N$ satisfy the condition, then for $N+1$ , we let $A_{N++}=A_N\cup \{N++\},B_{N++}=B_N\backslash \{N++\}$ , then for $A_{N++}$ and $B_{N++}$ condition (a)-(c) is easy to verify. By (d) and (e) we have $(N++)++\in B_{N++}$ , also condition (e) and (f) is easy to verify. The last two conditions also guarantees the uniqueness of $A_{N++}$ and $B_{N++}$ .
Step 3: use Axiom 2.5, we can say the final conclusion is true.
Next, the result in the exercise can be proved by substituting $\{n\in \mathbf N:n\leq N\}$ with $A_N$ .

$\blacksquare$

Exercises 3.5.13. The purpose of this exercise is to show that there is essentially only one version of the natural number system in set theory (cf. the discussion in Remark 2.1.12). Suppose we have a set $\mathbf N'$ of “alternative natural numbers”, an “alternative zero” $0'$ , and an “alternative increment operation” which takes any alternative natural number $n'\in \mathbf N'$ and returns another alternative natural number $n'++'\in\mathbf N'$ , such that the Peano axioms (Axioms 2.1-2.5) all hold with the natural numbers, zero, and increment replaced by their alternative counterparts. Show that there exists a bijection $f:\mathbf N \to \mathbf N'$ from the natural numebrs to the alternative natural numbers such that $f(0)=0'$ , and such that for any $n\in \mathbf N$ and $n'\in \mathbf N'$ , we have $f(n)=n'$ if and only if $f(n++)=n'++'$ .

Solution:
Let f be defined as follows:

$f(0)=0',\quad f(n++)=f(n)++',\quad \forall n\in \mathbf N$

Then $f(n)=n'\iff f(n++)=n'++'$ , we have to show $f$ is a function and bijective.
For any $n\in \mathbf N$ , use induction to prove $f(n)$ is unique(thus $f$ is a function). If $n=0$ then we can only have one $f(0)$ by definition. suppose $n>0$ and the hypothesis is true, then for $f(n++)$ , if there’s two numbers $a,b\in N',a\neq b$ such that $f(n++)=a,f(n++)=b$ , then we have $f(n)++'=a,f(n)++'=b$ , since $\mathbf N'$ obeys Peano Axioms, this means $f(n)$ must have two different values, a contradiction to the induction hypothesis.

To show $f$ is injective, let $f(n)=f(m),m,m\in \mathbf N$ , if $f(n)=f(m)=0'$ then we have $m=n=0$ , if $f(n)=f(m)=n'\neq 0'$ , then obviously $n\neq 0,m\neq 0$ , and we have

$a,b\in \mathbf N,a++=n,b++=m,\quad f(a)++'=f(b)++'$

This means $f(a)=f(b)$ , so assume $n\neq m$ , and without loss of general $n0$ , we can deduce that $f(0)=f(d)=0'$ . As $d>0,\exists e\in N,e++=d$ , then $f(d)=f(e)++'=0'$ .
This violates Peano Axiom 3.

To show $f$ is surjective, given $\forall n'\in \mathbf N'$ , if $n'=0'$ , we have $f(0)=n'$ , if $n'>0'$ , there’s $m'\in N',m'++'=n'$ , use induction we can assume for every alternative natural number less than $n'$ , there’s a natural number whose image is the given alternative natural number, so there’s $m\in \mathbf N,f(m)=m'$ , so $f(m++)=f(m)++'=n'$ , and $m++\in \mathbf N$ , which proves the induction.

$\blacksquare$

	匿名发表在《陶哲轩实分析（下）7.2及习题-Analysis II 7.…》
	swimming5cc5e307af发表在《陶哲轩实分析11.2及习题-Analysis I 11.2》
	匿名发表在《陶哲轩实分析3.4及习题-Analysis I 3.4》
	匿名发表在《陶哲轩实分析9.9及习题-Analysis I 9.9》
	匿名发表在《陶哲轩实分析（下）1.2及习题-Analysis II 1.…》