这一节的内容不长但是证明很难。核心目的是证明 可以成为有限个cyclic space的直和。首先介绍了
可以成为有限个cyclic space的直和。首先介绍了 -admissible的定义,是一个比invariant更强的定义,其能够保证多项式运算在子空间中有对应的分项(投影),Theorem 3是Cyclic Decomposition Theorem,与之前的Primary Decomposition Theorem相比,其说明
-admissible的定义,是一个比invariant更强的定义,其能够保证多项式运算在子空间中有对应的分项(投影),Theorem 3是Cyclic Decomposition Theorem,与之前的Primary Decomposition Theorem相比,其说明 可以成为惟一的有限个
可以成为惟一的有限个 -admissible space的直和,且每个子空间都是一个cyclic space,其generator的
-admissible space的直和,且每个子空间都是一个cyclic space,其generator的 -annihilator是可以递归整除的。在本节的前文中,作者称这个定理是one of the deepest results in linear algebra,证明确实非常繁复。这一定理有一系列重要的推论,例如每一个
-annihilator是可以递归整除的。在本节的前文中,作者称这个定理是one of the deepest results in linear algebra,证明确实非常繁复。这一定理有一系列重要的推论,例如每一个 -admissible空间都有一个invariant的互补空间。Theorem 4是广义的Cayley-Hamiltion定理,在之前的最小多项式整除特征多项式的结论之上,还可以推出二者有相同的prime factors,且已知最小多项式就可以得出特征多项式。Theorem 5声明每个矩阵都相似于一个唯一的rational form的矩阵。
-admissible空间都有一个invariant的互补空间。Theorem 4是广义的Cayley-Hamiltion定理,在之前的最小多项式整除特征多项式的结论之上,还可以推出二者有相同的prime factors,且已知最小多项式就可以得出特征多项式。Theorem 5声明每个矩阵都相似于一个唯一的rational form的矩阵。
Exercises
1.Let  be the linear operator on
be the linear operator on  which is represented in the standard ordered basis by the matrix
which is represented in the standard ordered basis by the matrix  . Let
. Let  . Show that
. Show that  , and that there is no non-zero vector
, and that there is no non-zero vector  in
in  with
with  disjoint from
disjoint from  .
.
Solution: We have

thus  , which means
, which means  , so
, so  .
.
Suppose there is some  such that
such that  is disjoint from
is disjoint from  , then
, then  , which means
, which means  or
or  , so
, so  , but this means
, but this means  , which contradicts the hypothesis that
, which contradicts the hypothesis that  is disjoint from
is disjoint from  .
.
2.Let  be a linear operator on the finite-dimensional space
be a linear operator on the finite-dimensional space  , and let
, and let  be the range of
be the range of  .
.
( a ) Prove that  has a complementary
has a complementary  -invariant subspace if and only if
-invariant subspace if and only if  is independent of the null space
is independent of the null space 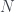 of
of  .
.
( b ) If  and
and 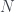 are independent, prove that
are independent, prove that 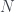 is the unique
is the unique  -invariant subspace complementary to
-invariant subspace complementary to  .
.
Solution:
( a ) If  is independent of
is independent of 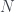 , then from
, then from  we know that
we know that  , and
, and 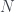 is obviously
is obviously  -invariant. Conversely, if
-invariant. Conversely, if  has a complementary
has a complementary  -invariant subspace
-invariant subspace  , let
, let  , then
, then  , but also
, but also  , thus
, thus  and
and  , so
, so  , since
, since  , we know
, we know  and so
and so  .
.
( b ) Let  be any
be any  -invariant subspace complementary to
-invariant subspace complementary to  , from the prood of (a) we can see that
, from the prood of (a) we can see that  , given
, given  and
and 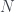 are independent.
are independent.
3.Let  be the linear operator on
be the linear operator on  which is represented in the standard ordered basis by the matrix
which is represented in the standard ordered basis by the matrix

Let 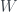 be the null space of
be the null space of  . Prove that
. Prove that 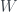 has no complementary
has no complementary  -invariant subspace.
-invariant subspace.
Solution: Assume there exists a  -invariant subspace
-invariant subspace  of
of  such that
such that  , then let
, then let  , we have
, we have  , since
, since  we see that
we see that  . On the other hand, since
. On the other hand, since  , we can find
, we can find  such that
such that  , so
, so

Since  is
is  -invariant, we see that
-invariant, we see that  and
and  , but
, but  means
means  , but
, but  , this is a contradiction.
, this is a contradiction.
4.Let  be the linear operator on
be the linear operator on  which is represented in the standard ordered basis by the matrix
which is represented in the standard ordered basis by the matrix

Let 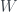 be the null space of
be the null space of  .
.
( a ) Prove that 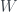 is the subspace spanned by
is the subspace spanned by  .
.
( b ) Find the monic generators of the ideals  ,
, ,
, ,
, .
.
Solution:
( a ) A direct computation shows that the matrix of  in the standard ordered basis is the matrix
in the standard ordered basis is the matrix

and we have  , thus
, thus 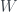 consists of all vectors of the form
consists of all vectors of the form  .
.
( b ) As  is already in
is already in 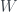 , we have
, we have  for all
for all ![f\in F[x]](https://s0.wp.com/latex.php?latex=f%5Cin+F%5Bx%5D&bg=ffffff&fg=333A42&s=0&c=20201002) , thus the monic generator of
, thus the monic generator of  is
is 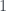 .
.
We have  , so the monic generator of
, so the monic generator of  is
is  . By the same logic, the monic generator of
. By the same logic, the monic generator of  is
is 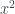 and the monic generator of
and the monic generator of  is
is  .
.
5.Let  be a linear operator on the vector space
be a linear operator on the vector space  over the field
over the field  . If
. If  is a polynomial over
is a polynomial over  and
and  , let
, let  . If
. If  are
are  -invariable subspaces and
-invariable subspaces and  , show that
, show that  .
.
Solution: For  , we have
, we have  , in which
, in which  for
for  , so
, so

this shows  . To see the sum is a direct sum, let
. To see the sum is a direct sum, let  with
with  , then we can find
, then we can find  such that
such that  , since
, since  and
and  are
are  -invariant, we have
-invariant, we have  and
and  , so
, so  and
and  , this shows
, this shows  and
and  are independent.
are independent.
6.Let  be as in Exercise 5. Suppose
be as in Exercise 5. Suppose  and
and  are vectors in
are vectors in  which have the same
which have the same  -annihilator. Prove that, for any polynomial
-annihilator. Prove that, for any polynomial  , the vectors
, the vectors  and
and  have the same
have the same  -annihilator.
-annihilator.
Solution: Let 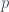 be the
be the  -annihilator of both
-annihilator of both  and
and  . Suppose the
. Suppose the  -annihilator of
-annihilator of  is
is  , then
, then  , which means
, which means  is in the ideal generated by
is in the ideal generated by 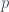 , so we can find polynomial
, so we can find polynomial 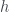 such that
such that  , this means
, this means  , thus the
, thus the  -annihilator of
-annihilator of  divides
divides  , with the same logic applying to the
, with the same logic applying to the  -annihilator of
-annihilator of  , we see
, we see  divides the
divides the  -annihilator of
-annihilator of  , thus they are the same.
, thus they are the same.
7.Find the minimal polynomials and the rational forms of each of the following real matrices.

Solution: For the first matrix, we compute the characteristic polynomial

and the minimal polynomial is also  . Thus the rational form of this matrix is
. Thus the rational form of this matrix is

For the second matrix we compute the characteristic polynomial
![\displaystyle{\begin{aligned}\begin{vmatrix}x-c&0&1\\0&x-c&-1\\1&-1&x-c\end{vmatrix}&=(x-c)[(x-c)^2-1]-(x-c)\\&=(x-c)[(x-c)^2-2]\\&=x^3-3cx^2+(3c^2-2)x-c^3+2c\end{aligned}}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%7B%5Cbegin%7Baligned%7D%5Cbegin%7Bvmatrix%7Dx-c%260%261%5C%5C0%26x-c%26-1%5C%5C1%26-1%26x-c%5Cend%7Bvmatrix%7D%26%3D%28x-c%29%5B%28x-c%29%5E2-1%5D-%28x-c%29%5C%5C%26%3D%28x-c%29%5B%28x-c%29%5E2-2%5D%5C%5C%26%3Dx%5E3-3cx%5E2%2B%283c%5E2-2%29x-c%5E3%2B2c%5Cend%7Baligned%7D%7D&bg=ffffff&fg=333A42&s=0&c=20201002)
and the minimal polynomial is also  . Thus the rational form of this matrix is
. Thus the rational form of this matrix is

For the third matrix we compute the characteristic polynomial

and the minimal polynomial is also  . Thus the rational form of this matrix is
. Thus the rational form of this matrix is  .
.
8.Let  be the linear operator on
be the linear operator on  which is represented in the standard basis by
which is represented in the standard basis by

Find non-zero vectors  satisfying the conditions of Theorem 3.
satisfying the conditions of Theorem 3.
Solution: We first compute the characteristic polynomial of  :
:

Now the matrix of  is obviously not zero and the matrix of
is obviously not zero and the matrix of  is
is

thus the minimal polynomial for  is
is  . Since
. Since  which is not a scalar multiple of
which is not a scalar multiple of  ,
,  has dimension 2 and consists of all vectors
has dimension 2 and consists of all vectors

So we can let  , the vector
, the vector  must be a characteristic vector of
must be a characteristic vector of  which is not in
which is not in  , As we can see if
, As we can see if  , then
, then  means
means  is in the form
is in the form  , let
, let  we see that we can make
we see that we can make  .
.
9.Let  be the real matrix
be the real matrix

Find an invertible  real matrix
real matrix  such that
such that  is in rational form.
is in rational form.
Solution: First compute the characteristic polynomial for 

and since

the minimal polynomial for  is
is  .
.
Since  is not a scalar multiple of
is not a scalar multiple of  , one subspace can be
, one subspace can be  , which consists of vectors like
, which consists of vectors like  , choose a characteristic vector associated with the characteristic value
, choose a characteristic vector associated with the characteristic value  , which may be
, which may be  , then let
, then let

we have  , thus
, thus  is invertible, and
is invertible, and

the rational form of  is clearly
is clearly  , and we have
, and we have

thus  is the matrix we need.
is the matrix we need.
10.Let  be a subfield of the complex numbers and let
be a subfield of the complex numbers and let  be the linear operator on
be the linear operator on  which is represented in the standard ordered basis by the matrix
which is represented in the standard ordered basis by the matrix

Find the characteristic polynomial for  . Consider the cases
. Consider the cases  ;
;  ;
;  . In each of these cases, find the minimal polynomial for
. In each of these cases, find the minimal polynomial for  and non-zero vectors
and non-zero vectors  which satisfy the conditions of Theorem 3.
which satisfy the conditions of Theorem 3.
Solution: The characteristic polynomial for  is
is  .
.
In the case  , the minimal polynomial for
, the minimal polynomial for  is
is  , since for
, since for  , we have
, we have  ,
,  ,
,  , we have
, we have  .
.
In the case  and
and  , the minimal polynomial for
, the minimal polynomial for  is
is  . The non-zero vectors
. The non-zero vectors  satisfing Theorem 3 can be found using techniques in the proof of Theorem 3.
satisfing Theorem 3 can be found using techniques in the proof of Theorem 3.
11.Prove that if  and
and  are
are  matrices over a field
matrices over a field  , a necessary and sufficient condition that
, a necessary and sufficient condition that  and
and  be similar over
be similar over  is that they have the same characteristic polynomial and the same minimal polynomial. Give an example which shows that this is false for
is that they have the same characteristic polynomial and the same minimal polynomial. Give an example which shows that this is false for  matrices.
matrices.
Solution: If  and
and  are similar, then both are similar to the same matrix
are similar, then both are similar to the same matrix  which is in rational form, thus the minimal polynomial for
which is in rational form, thus the minimal polynomial for  and
and  are the same. Let it be
are the same. Let it be 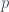 .
.
If  , then it is the characteristic polynomial for both
, then it is the characteristic polynomial for both  and
and  .
.
If  , then
, then  must have the form
must have the form  , where
, where  is a
is a  matrix in the rational form, then the characteristic polynomial for
matrix in the rational form, then the characteristic polynomial for  and
and  are
are  .
.
If  , then
, then  must be diagonal, then it is apparent the characteristic polynomial for
must be diagonal, then it is apparent the characteristic polynomial for  and
and  are equal.
are equal.
Conversely, if  and
and  have the same characteristic polynomial
have the same characteristic polynomial  and the same minimal polynomial
and the same minimal polynomial 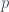 . We find the unique matrix in the rational form that
. We find the unique matrix in the rational form that  and
and  are similar to, namely
are similar to, namely  and
and  , then
, then
If  , then we must have
, then we must have  .
.
If  , then
, then  ,
,  , where
, where  is a
is a  matrix in the rational form, and
matrix in the rational form, and  means
means  , so
, so  .
.
If  , then
, then  and
and  must be diagonal, since the characteristic polynomial for
must be diagonal, since the characteristic polynomial for  and
and  are equal ,we have
are equal ,we have  .
.
Since  is similar to
is similar to  and
and  is similar to
is similar to  , we have
, we have  similar to
similar to  .
.
For a counterexample of  matrix, we let
matrix, we let

The characteristic polynomial of  and
and  is
is  , the minimal polynomial of
, the minimal polynomial of  and
and  is
is  , but
, but  and
and  are not similar.
are not similar.
12.Let  be a subfield of the field of complex numbers, and let
be a subfield of the field of complex numbers, and let  and
and  be
be  matrices over
matrices over  . Prove that if
. Prove that if  and
and  are similar over the field of complex numbers, then they are similar over
are similar over the field of complex numbers, then they are similar over  .
.
Solution: The rational form of  is a matrix over
is a matrix over  , thus a matrix over
, thus a matrix over 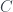 , likewise for
, likewise for  . Thus if
. Thus if  and
and  are similar over the field of complex numbers, due to Theorem 5, the rational form of
are similar over the field of complex numbers, due to Theorem 5, the rational form of  is the same as
is the same as  over
over 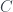 , which means
, which means  and
and  are similar to the same rational form over
are similar to the same rational form over  , and the conclusion follows.
, and the conclusion follows.
13.Let  be an
be an  matrix with complex entires. Prove that if every characteristic value of
matrix with complex entires. Prove that if every characteristic value of  is real, then
is real, then  is similar to a matrix with real entries.
is similar to a matrix with real entries.
Solution: The characteristic polynomial for  contains only linear factors, and so is the minimal polynomial
contains only linear factors, and so is the minimal polynomial 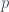 for
for  , since every characteristic value of
, since every characteristic value of  is real, we see
is real, we see 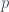 consists only real coefficients.
consists only real coefficients.
Let  be the linear operator on
be the linear operator on  which is represented by
which is represented by  in the standard basis, then there is an ordered basis
in the standard basis, then there is an ordered basis  for
for  such that
such that
![\displaystyle{[T]_{\mathfrak B}=\begin{bmatrix}A_1\\&A_2\\&&{\ddots}\\&&&&A_r\end{bmatrix}}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%7B%5BT%5D_%7B%5Cmathfrak+B%7D%3D%5Cbegin%7Bbmatrix%7DA_1%5C%5C%26A_2%5C%5C%26%26%7B%5Cddots%7D%5C%5C%26%26%26%26A_r%5Cend%7Bbmatrix%7D%7D&bg=ffffff&fg=333A42&s=0&c=20201002)
where each  is the companion matrix of some polynomial
is the companion matrix of some polynomial  , and
, and  , and
, and  for
for  , since
, since 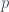 consists only real coefficients, so are all
consists only real coefficients, so are all  , which means all
, which means all  have real entries, and so is
have real entries, and so is ![[T]_{\mathfrak B}](https://s0.wp.com/latex.php?latex=%5BT%5D_%7B%5Cmathfrak+B%7D&bg=ffffff&fg=333A42&s=0&c=20201002) , apparently,
, apparently,  is similar to
is similar to ![[T]_{\mathfrak B}](https://s0.wp.com/latex.php?latex=%5BT%5D_%7B%5Cmathfrak+B%7D&bg=ffffff&fg=333A42&s=0&c=20201002) .
.
14.Let  be a linear operator on the finite-dimensional space
be a linear operator on the finite-dimensional space  . Prove that there exists a vector
. Prove that there exists a vector  with this property. If
with this property. If  is a polynomial and
is a polynomial and  , then
, then  . (Such a vector
. (Such a vector  is called a separating vector for the algebra of polynomials in
is called a separating vector for the algebra of polynomials in  .) When
.) When  has a cyclic vector, give a direct proof that any cyclic vector is a separating vector for the algebra of polynomials in
has a cyclic vector, give a direct proof that any cyclic vector is a separating vector for the algebra of polynomials in  .
.
Solution: We first prove if  is a cyclic vector of
is a cyclic vector of  , then
, then  is a separating vector for the algebra of polynomials in
is a separating vector for the algebra of polynomials in  . Suppose
. Suppose  , then
, then  span
span  , so for any
, so for any  , we have
, we have  for some polynomial
for some polynomial 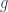 . Now if
. Now if  is a polynomial and
is a polynomial and  , we have
, we have

thus  .
.
Now for any linear operator  on
on  , use the Cyclic Decomposition Theorem, we can write
, use the Cyclic Decomposition Theorem, we can write  , let
, let  , then
, then  means
means  since each
since each  is invariant under
is invariant under  , and
, and  is the direct sum of all
is the direct sum of all  . It follows that
. It follows that  on
on  for
for  , which means
, which means  on
on  .
.
15.Let  be a subfield of the field of complex numbers, and let
be a subfield of the field of complex numbers, and let  be an
be an  matrix over
matrix over  . Let
. Let 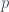 be the minimal polynomial for
be the minimal polynomial for  . If we regard
. If we regard  as a matrix over
as a matrix over 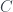 , then
, then  has a minimal polynomial
has a minimal polynomial  as an
as an  matrix over
matrix over 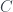 . Use a theorem on linear equations to prove
. Use a theorem on linear equations to prove  . Can you also see how this follows from the cyclic decomposition theorem?
. Can you also see how this follows from the cyclic decomposition theorem?
Solution: If we write  , then
, then  means
means  is a solution for the system
is a solution for the system

in the field  , and likewise,
, and likewise,  is the polynomial which has coefficients
is the polynomial which has coefficients  as a solution for the same system in the field
as a solution for the same system in the field 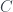 , then
, then  is a solution in
is a solution in  due to the final remark in Sec 1.4. Thus both
due to the final remark in Sec 1.4. Thus both  and
and  are in the solution space for
are in the solution space for  . To prove
. To prove  , assume there is some
, assume there is some  , then
, then  is a non-trivial solution for the system
is a non-trivial solution for the system

Let  and
and  , we see
, we see  , but
, but  , a contradiction.
, a contradiction.
To get this result from the cyclic decomposition theorem, notice that by Exercise 12,  has the same rational form in
has the same rational form in  and
and 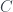 , and the first block matrix of the rational form of
, and the first block matrix of the rational form of  is the companion matrix of
is the companion matrix of 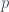 in
in  and
and  in
in 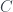 , we have
, we have  .
.
16.Let  be an
be an  matrix with real entries such that
matrix with real entries such that  . Prove that
. Prove that  is even, and if
is even, and if  , then
, then  is similar over the field of real numbers to a matrix of the block form
is similar over the field of real numbers to a matrix of the block form  where
where  is the
is the  identity matrix.
identity matrix.
Solution: The minimal polynomial for  is
is  , by the generalized Cayley-Hamilton Theorem, the characteristic polynomial for
, by the generalized Cayley-Hamilton Theorem, the characteristic polynomial for  must be of the form
must be of the form  , so
, so  is even.
is even.
If  , we know
, we know  is similar to one and only one matrix
is similar to one and only one matrix  in the rational form. If we write
in the rational form. If we write

where each  is the companion matrix of
is the companion matrix of  , and
, and  divides
divides  , from the proof of Theorem 3 we know
, from the proof of Theorem 3 we know  , and the only possible polynomial which divides
, and the only possible polynomial which divides  is
is  and
and 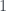 . Since
. Since 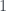 can only be the annihilator of zero vectors, we see that
can only be the annihilator of zero vectors, we see that

Let  be a basis for
be a basis for  and
and  is the linear operator with
is the linear operator with ![[T]_{\mathscr B}=B](https://s0.wp.com/latex.php?latex=%5BT%5D_%7B%5Cmathscr+B%7D%3DB&bg=ffffff&fg=333A42&s=0&c=20201002) , then
, then

If we let  for
for  and
and  for
for  , then
, then  is a basis for
is a basis for  , and we can verify
, and we can verify ![[T]_{\mathscr B'}=\begin{bmatrix}0&-I\\I&0\end{bmatrix}](https://s0.wp.com/latex.php?latex=%5BT%5D_%7B%5Cmathscr+B%27%7D%3D%5Cbegin%7Bbmatrix%7D0%26-I%5C%5CI%260%5Cend%7Bbmatrix%7D&bg=ffffff&fg=333A42&s=0&c=20201002) , which means
, which means  is similar to
is similar to  and so is
and so is  .
.
17.Let  be a linear operator on a finite-dimensional vector space
be a linear operator on a finite-dimensional vector space  . Suppose that
. Suppose that
( a ) the minimal polynomial for  is a power of an irreducible polynomial;
is a power of an irreducible polynomial;
( b ) the minimal polynomial is equal to the characteristic polynomial.
Show that no non-trivial  -invariant subspace has a complementary
-invariant subspace has a complementary  -invariant subspace.
-invariant subspace.
Solution: Let 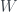 be a non-trivial
be a non-trivial  -invariant subspace of
-invariant subspace of  , assume there is
, assume there is  which is
which is  -invariant such that
-invariant such that  , let
, let  and
and  , then the minimal polynomial
, then the minimal polynomial 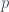 of
of  and
and  of
of  divide the minimal polynomial for
divide the minimal polynomial for  . Since the minimal polynomial for
. Since the minimal polynomial for  is of the form
is of the form  where
where  is irreducible, we have
is irreducible, we have  and
and  , where
, where  . As
. As 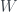 is non-trivial, we have
is non-trivial, we have  .
.
Now if  , we can get a contradiction by the following procedure: from (b) we know that
, we can get a contradiction by the following procedure: from (b) we know that  has a cyclic vector
has a cyclic vector  such that the
such that the  -annihilator of
-annihilator of  is
is  , and there is
, and there is  such that
such that  , we let
, we let  , then
, then  , and
, and  , which means
, which means  , this is a contradiction.
, this is a contradiction.
Thus 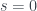 , or the minimal polynomial for
, or the minimal polynomial for  is
is 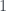 , which means
, which means  or
or  .
.
18.If  is a diagonalizable linear operator, then every
is a diagonalizable linear operator, then every  -invariant subspace has a complementary
-invariant subspace has a complementary  -invariant subspace.
-invariant subspace.
Solution:  is diagonalizable means if we let
is diagonalizable means if we let  be distinct characteristic values of
be distinct characteristic values of  and let
and let  , then
, then

Let 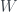 be a
be a  -invariant subspace of
-invariant subspace of  , then by Exercise 10 of Section 6.8, we have
, then by Exercise 10 of Section 6.8, we have

Consider  , for any
, for any  , we have
, we have  , so
, so  . Since
. Since  is a subspace, we can find
is a subspace, we can find  to be a basis for it, then it can be extended to a basis for
to be a basis for it, then it can be extended to a basis for  , namely
, namely  , all of which are characteristic vectors associated with
, all of which are characteristic vectors associated with  . Let
. Let  be the space spanned by
be the space spanned by  , then
, then  , let
, let  , we see that
, we see that  , and as each
, and as each  is invariant under
is invariant under  , so is
, so is  .
.
19.Let  be a linear operator on the finite-dimensional space
be a linear operator on the finite-dimensional space  . Prove that
. Prove that  has a cyclic vector if and only if the following is true: Every linear operator
has a cyclic vector if and only if the following is true: Every linear operator  which commutes with
which commutes with  is a polynomial in
is a polynomial in  .
.
Solution: First suppose  is a cyclic vector of
is a cyclic vector of  , then if
, then if  , we have
, we have  being a basis for
being a basis for  . Given an operator
. Given an operator  which commutes with
which commutes with  , we have
, we have

where  , notice that
, notice that

We can see that  on a basis for
on a basis for  , thus on
, thus on  .
.
Conversely, if every linear operator  which commutes with
which commutes with  is a polynomial in
is a polynomial in  , let the cyclic decomposition of
, let the cyclic decomposition of  by
by  be
be

and  is the
is the  -annihilator for
-annihilator for  with
with  . Define
. Define  as follows:
as follows:  if
if  and
and  if
if  . For any
. For any  , we have
, we have  where each
where each  , so
, so

Then  commutes with
commutes with  , thus is a polynomial for
, thus is a polynomial for  . Let
. Let  , since
, since  , we know
, we know  , which means
, which means  for
for  , so
, so  for
for  , which means
, which means  for
for  , so
, so  and
and  has a cyclic vector.
has a cyclic vector.
20.Let  be a finite-dimensional vector space over the field
be a finite-dimensional vector space over the field  , and let
, and let  be a linear operator on
be a linear operator on  . We ask when it is true that every non-zero vector in
. We ask when it is true that every non-zero vector in  is a cyclic vector for
is a cyclic vector for  . Prove that this is the case if and only if the characteristic polynomial for
. Prove that this is the case if and only if the characteristic polynomial for  is irreducible over
is irreducible over  .
.
Solution: Let  . First suppose the characteristic polynomial
. First suppose the characteristic polynomial  for
for  is irreducible over
is irreducible over  , then by the Generalized Cayley-Hamiltion Theorem, the minimal polynomial
, then by the Generalized Cayley-Hamiltion Theorem, the minimal polynomial 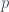 for
for  is equal to
is equal to  and irreducible over
and irreducible over  . For any nonzero vector
. For any nonzero vector  , if
, if  is linearly dependent, then there is
is linearly dependent, then there is ![g\in F[x]](https://s0.wp.com/latex.php?latex=g%5Cin+F%5Bx%5D&bg=ffffff&fg=333A42&s=0&c=20201002) with
with  , since
, since  , we see
, we see  , a contradiction to
, a contradiction to 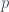 being irreducible. Then it means
being irreducible. Then it means  is linearly independent, or
is linearly independent, or  .
.
Conversely, if every non-zero vector in  is a cyclic vector for
is a cyclic vector for  , and assume the characteristic polynomial
, and assume the characteristic polynomial  for
for  is not irreducible over
is not irreducible over  , then if the minimal polynomial
, then if the minimal polynomial 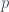 for
for  is not the same as
is not the same as  , we have
, we have  , there is a vector
, there is a vector  such that the
such that the  -annihilator for
-annihilator for  is
is 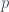 , so
, so  has dimension
has dimension  , which means
, which means  is not a cyclic vector for
is not a cyclic vector for  .
.
If  and
and  where
where  , then it is apparent
, then it is apparent  , let
, let  , there is a vector
, there is a vector  such that the
such that the  -annihilator for
-annihilator for  is
is 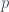 , thus
, thus  , and
, and  . Notice that
. Notice that

this shows  is linearly dependent, thus by Theorem 1,
is linearly dependent, thus by Theorem 1,  , so
, so  is not a cyclic vector for
is not a cyclic vector for  .
.
21.Let  be an
be an  matrix with real entries. Let
matrix with real entries. Let  be the linear operator on
be the linear operator on  which is represented by
which is represented by  in the standard ordered basis, and let
in the standard ordered basis, and let  be the linear operator on
be the linear operator on  which is represented by
which is represented by  in the standard ordered basis. Use the result of Exercise 20 to prove the following: If the only subspace invariant under
in the standard ordered basis. Use the result of Exercise 20 to prove the following: If the only subspace invariant under  are
are  and the zero subspace, then
and the zero subspace, then  is diagonalizable.
is diagonalizable.
Solution: Since  is real, the characteristic polynomial for
is real, the characteristic polynomial for  and
and  are equal, both are
are equal, both are  . Now given any nonzero vector
. Now given any nonzero vector  , the cyclic space
, the cyclic space  must be
must be  since it is invariant under
since it is invariant under  and contains
and contains  , so by Exercise 20,
, so by Exercise 20,  is irreducible over
is irreducible over  , which means
, which means  must be of the form
must be of the form  or
or  where
where  . Then in the field
. Then in the field 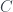 ,
,  can be factored into prime factors and thus
can be factored into prime factors and thus  is diagonalizable.
is diagonalizable.
and
be
nilpotent matrices over the field
. Prove that
and
are similar if and only if they have the same minimal polynomial.
and
are similar, then they are similar to the same matrix which is in the rational form, thus have the same minimal polynomial.
be the minimal polynomial for
and
, then since both are nilpotent,
can only be
or
. If
, then
and are similar. If
, then both
and
are similar to the matrix
.
, then both
and
are similar to the matrix
and
be
matrices over the field
which have the same characteristic polynomial
is greater than
, then
and
are similar.
and
are separately similar to the matrix
are
matrices. Since
is no greater than
, the minimal polynomial for
and
are the same, use Exercise 1 we know
is similar to
, and the conclusion follows.
is a complex
matrix with characteristic polynomial
, and minimal polynomial
, what is the Jordan form for
?
is
complex matrix with characteristic polynomial
?
, where
is
matrix and
is
matrix.
has two possible forms, corresponding to the minimal polynomial for the subspace
being
or
.
, if the minimal polynomial
for
is
, then
has only one form, the same when
and
. When
, there are two possible forms of
, namely
has 5 forms while
has 2, thus the possible forms for the original matrix is 10.
is represented in the ‘natural’ ordered basis by the matrix
a subfield of the complex numnbers.)
be the differentiation operator, then
and
is a nilpotent operator, since
, the Jordan form of this matrix is
be the complex matrix
.
is
, and
, and
, so the minimal polynomial for
is
. The Jordan form for
is
is an
matrix over the field
with characteristic polynomial
?
is similar to the Jordan form matrix, in which the trace is
.
complex matrices
such that
.
is all matrices which is similar to the diagonal matrix
.
complex matrices
such that
.
is all matrices which is similar to the diagonal matrix
, where
are the
-th unit root in the complex field.
be a positive integer,
, and let
be an
matrix over the field
such that
but
. Prove that
has no square root, i.e., that there is no
matrix
such that
.
, which means
is nilpotent, thus
, also
, which means
, or
, a contradiction.
and
be
nilpotent matrices over the field
. Suppose that
and
have the same minimal polynomial and the same nullity. Prove that
and
are similar. Show that this is not true for
nilpotent matrices.
and
have the same minimal polynomial
, also if we let
be the nullity for
and
, then the Jordan form of both
and
have
elementary Jordan matrix with characteristic value
. So all we need to do is check the possible arrangement of
forms under the condition
.
, the result is obvious.
, then
is at least
, when
the arrange is
, when
the arrange is
, when
the arrange is
, which are all unique.
, then
is at least
, when
the arrange is
, when
the arrange is
, when
the arrange is
, which are all unique.
, then
is at least
, when
the arrange is
, when
the arrange is
, which are all unique.
then
, the arrange is
.
, then
and there is only one elementary Jordan matrix.
and
are the same, thus they are similar.
matrix, let
and
are
and the nullity are
, but they are not similar.
and
be
matrices over the field
which have the same characteristic polynomial
the solution space of
and
have the same dimension. If no
is greater than
, then
and
are similar.
and
are separately similar to the matrix
are
matrices. For each
, the nilpotent matrix
and
have the same minimal polynomial and the same nullity, since
, they are similar and so for some invertible
matrix
we have
and
are similar.
is a
elementary nilpotent matrix, i.e.,
but
, show that
is similar to
. Now use the Jordan form to prove that every complex
matrix is similar to its transpose.
is
and thus the Jordan form for
is the
matrix
, we also have
and
, so
shall also be similar to
.
is a complex
matrix such that
, then
. (Proof: Let
be the Jordan form of
. Since
. But
is triangular so that
implies that every entry of
is zero. Since
and
is similar to
, we see that
.) (Give an example of a non-zero
such that
.)
. The problem with the proof is that
does not imply
.
is a nilpotent
matrix over
, prove that
satisfy
, i.e.,
is a square root of
. Use the binomial series for
to obtain a similar formula for a square root of
, where
is any nilpotent
matrix over
.
and then
where
is a
nilpotent matrix can be
is a non-zero complex number and
is a nilpotent complex matrix, then
has a square root. Now use the Jordan form to prove that every non-singular complex
matrix has a square root.
we can have
, also if
is nilpotent we have
being nilpotent, so by Exercise 15,
has a square root, namely
, consider
, we have
has a square root.
be any non-singular complex
matrix, the characteristic polynomial for
shall be
for all
and
. The Jordan form of
is of the form
is a
matrix consisting of some elementary Jordan matrix associated with
and
for some invertible
matrix
. Notice that
is nlipotent, thus
has a square root, namely
, if we let
, which means
.